[next] [prev] [prev-tail] [tail] [up]

C From (δΦ,δA) to (δE,δB)

C.1 Expression of δB⊥ in terms of δA

Note that

δB ⊥ = ∇ × δA − (e∥ ⋅∇ × δA)e∥ = ∇ × (δA + δA e )− [e ⋅∇ × (δA + δA e )]e (306) ⊥ ∥ ∥ ∥ ⊥ ∥ ∥ ∥
Correct to order O(λ), δB⊥ in the above equation is written as (e∥ vector can be considered as constant because its spatial gradient combined with δA will give terms of O(λ2), which are neglected)
δB ≈ ∇ × δA +∇ δA × e − [e ⋅∇ × δA + e ⋅(∇δA × e )]e (307) ⊥ ⊥ ∥ ∥ ∥ ⊥ ∥ ∥ ∥ ∥ = ∇ × δA ⊥ +∇ δA∥ × e∥ − (e∥ ⋅∇ × δA⊥ )e∥ (308)
Using local cylindrical coordinates (r,ϕ,z) with z being along the local direction of B0, and two components of A⊥ being Ar and Aϕ, then ∇× A⊥ is written as
( ∂δA ) (∂δA ) 1 [ ∂ ∂δA ] ∇ × δA ⊥ = − ---ϕ- er + ----r eϕ +- --(rδAϕ)− ----r e∥. ∂z ∂z r ∂r ∂ ϕ
(309)

Note that the parallel gradient operator ∇∥≡ e∥⋅∇ = ∂∕∂z acting on the the perturbed quantities will result in quantities of order O(λ2). Retaining terms of order up to O(λ), equation (309) is written as

1 [ ∂ ∂ δA ] ∇ ×δA ⊥ ≈ - --(rδAϕ)− ----r e∥, r ∂r ∂ ϕ
(310)

i.e., only the parallel component survive, which exactly cancels the last term in Eq. (308), i.e., equation (308) is reduced to

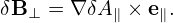δB⊥ = ∇ δA ∥ × e∥.
(311)

C.1.1 Using basis vectors in field-aligned coordinates

In terms of δBxL and δByL,  δB⊥ is written as

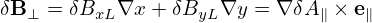δB ⊥ = δBxL∇x + δByL ∇y = ∇δA ∥ × e∥
(312)

Dotting the above equation by ∇x and ∇y, respectively, we obtain

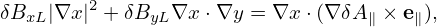δBxL|∇x|2 + δByL∇x ⋅∇y = ∇x ⋅(∇ δA∥ × e∥),
(313)

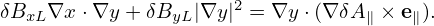2 δBxL∇x ⋅∇y + δByL|∇y |= ∇y ⋅(∇ δA∥ × e∥).
(314)

Equations (313) and (314) can be further written as

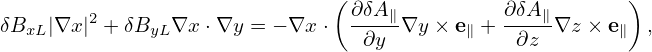( ) 2 ∂δA∥- ∂δA∥- δBxL|∇x| + δByL∇x ⋅∇y = − ∇x ⋅ ∂y ∇y × e∥ + ∂z ∇z × e∥ ,
(315)

and

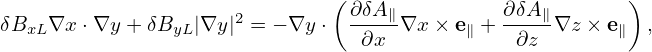( ) 2 ∂δA∥- ∂δA∥- δBxL∇x ⋅∇y + δByL |∇y | = − ∇y ⋅ ∂x ∇x × e∥ + ∂z ∇z × e∥ ,
(316)

The solution of this 2 × 2 system is expressed by Cramer’s rule in the code.

 

Use B0 = Ψ′∇x ×∇y

b = Ψ′∇x ×∇y∕B0

C.2 Expression of δB∥ in terms of δA

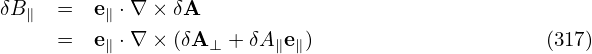
δB ∥ = e∥ ⋅∇ × δA = e∥ ⋅∇ × (δA⊥ + δA∥e∥) (317)
Accurate to O(λ1), δB∥ in the above equation is written as (e∥ vector can be considered as constant because its spatial gradient combined with δA will give O(λ2) terms, which are neglected)
δB∥ ≈ e∥ ⋅∇ ×δA ⊥ + e∥ ⋅(∇δA ∥ × e∥) = e∥ ⋅∇ ×δA ⊥ (318)
[Using local cylindrical coordinates (r,ϕ,z) with z being along the local direction of B0, and two components of δA⊥ being δAr and δAϕ, then ∇× δA⊥ is written as
( ) ( ) [ ] ∂δA-ϕ ∂δAr- 1 ∂-- ∂δAr- ∇ × δA⊥ = − ∂z er + ∂z er + r ∂r(rδAϕ)− ∂ϕ e∥
(319)

Note that the parallel gradient operator ∇∥≡ e∥⋅∇ = ∂∕∂z acting on the the perturbed quantities will result in quantities of order O(λ2). Retaining terms of order up to O(λ), equation (309) is written as

1 [ ∂ ∂ δA ] ∇ ×δA ⊥ ≈ - --(rδAϕ)− ----r e∥, r ∂r ∂ ϕ
(320)

Using this, equation (318) is written as

1[ ∂ ∂δA ] δB∥ = - --(rδA ϕ)− ----r . r ∂r ∂ϕ
(321)

However, this expression is not useful for GEM because GEM does not use the local coordinates (r,ϕ,z).]

 

C.3 Expressing the perturbed drift in terms of δE and δB

The perturbed drift δVD is given by Eq. (138), i.e.,

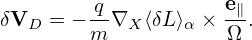e δVD = −-q∇X ⟨δL⟩α × -∥. m Ω
(322)

Using δL = δΦ − v ⋅ δA, the above expression can be further written as

e δVD = − q-∇X ⟨δΦ − v ⋅δA⟩α × -∥ qme qe Ω = ---∥ × ∇X ⟨δΦ⟩α −---∥ × ∇X ⟨v∥δA ∥⟩α m qΩe∥ m Ω − m-Ω-× ∇X ⟨v⊥ ⋅δA⊥ ⟩α. (323)
Accurate to order O(λ), the term involving δΦ is
q-e∥ × ∇X ⟨δΦ ⟩α = e∥-× ⟨∇X δΦ⟩α m Ω B0 ≈ e∥-× ⟨∇xδΦ⟩α B0 ⟨ ⟩ ≈ e∥-× − δE − ∂δA- B0 ∂t α e∥- ≈ B0 × ⟨− δE⟩α ≡ δVE, (324)
which is the δE×B0 drift. Accurate to O(λ), the ⟨v∥δA∥⟩α term on the right-hand side of Eq. (323) is written
e v − q--∥ × ∇X ⟨v∥δA ∥⟩α ≈ −-q-∥⟨e∥ × ∇X (δA∥)⟩α m Ω mqvΩ ≈ −---∥⟨e∥ × ∇x (δA∥)⟩α (325) m Ω = v∥ ⟨δB-⊥⟩α, (326) B0
which is called “magnetic fluttering” (this is actually not a real drift). In obtaining the last equality, use has been made of Eq. (311), i.e., δB⊥ = ∇xδA∥× e∥.

Accurate to O(λ), the last term on the right-hand side of expression (323) is written

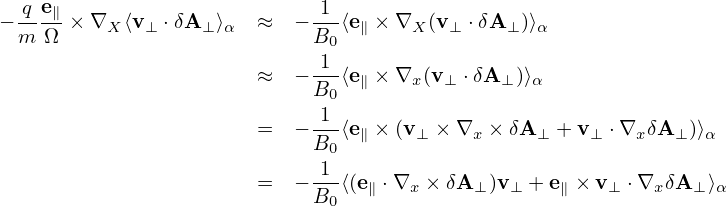
-qe∥ -1- − m Ω × ∇X ⟨v⊥ ⋅δA ⊥⟩α ≈ − B0 ⟨e∥ ×∇X (v⊥ ⋅δA ⊥)⟩α 1 ≈ − B--⟨e∥ ×∇x (v⊥ ⋅δA⊥)⟩α 01 = − ---⟨e∥ ×(v⊥ × ∇x × δA⊥ + v⊥ ⋅∇xδA ⊥)⟩α B0 = − -1-⟨(e∥ ⋅∇x × δA ⊥)v⊥ + e∥ × v⊥ ⋅∇xδA ⊥⟩α B0
Using equation (318), i.e., δB∥ = e∥⋅∇× δA⊥, the above expression is written as
− q-e∥ × ∇X ⟨v ⊥ ⋅δA ⊥⟩α = − -1⟨δB ∥v ⊥ + e∥ ×v ⊥ ⋅∇x δA⊥ ⟩α m Ω B0 ≈ − -1⟨δB v + e ×v ⋅∇ δA ⟩ B0 ∥ ⊥ ∥ ⊥ X ⊥ α -1- -1- ≈ − B0⟨δB ∥v ⊥⟩α − B0 e∥ × ⟨v⊥ ⋅∇X δA⊥⟩α. -1- ≈ − B0⟨δB ∥v ⊥⟩α. (327)
where use has been made of ⟨v⊥⋅∇XδA⊥⟩α ≈ 0 (**seems wrong**), where the error is of O(λ)δA⊥. The term ⟨δB∥v⊥⟩α∕B0 is of O(λ2) and thus can be neglected (I need to verify this).

Using Eqs. (324), (326), and (327), expression (323) is finally written as

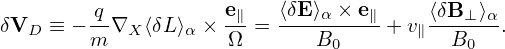q- e∥ ⟨δE⟩α ×-e∥ ⟨δB-⊥⟩α- δVD ≡ − m ∇X ⟨δL ⟩α × Ω = B0 + v∥ B0 .
(328)

Using this, the first equation of the characteristics, equation (292), is written as

dX- = v e + V + δV (329) dt ∥ ∥ D D ⟨δE-⟩α-×-e∥ ⟨δB⊥-⟩α- = v∥e∥ + VD + B0 + v∥ B0 ≡ VG (330)

C.4 Expressing the coefficient before ∂F0∕∂𝜀 in terms of δE and δB

[Note that

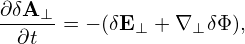∂δA⊥-= − (δE +∇ δΦ ), ∂t ⊥ ⊥
(331)

where ∂δA⊥∕∂t is of O(λ2). This means that δE⊥ + ∇⊥δϕ is of O(λ2) although both δE⊥ and δϕ are of O(λ).]

Note that

∂⟨v⋅δA-⟩α = v ∂⟨δA∥⟩α + v⊥ ⋅ ∂⟨δA⟩α ∂t ∥ ∂t ∂t ∂⟨δA∥⟩α = v∥ ∂t + ⟨v ⊥ ⋅(− δE − ∇ δΦ)⟩α ∂⟨δA∥⟩α ≈ v∥ ∂t − ⟨v ⊥ ⋅δE ⟩α (332)
where use has been made of ⟨v⊥⋅∇δϕ⟩≈ 0, This indicates that ⟨v⊥⋅ δE⟩α is of O(λ1)δE. Using Eq. (332), the coefficient before ∂F0∕∂𝜀 in Eq. (141) can be further written as
[ ( ) ] −-q − ∂⟨v-⋅δA⟩α − v e + V − -qe∥ × ∇ ⟨v⋅δA ⟩ ⋅∇ ⟨δΦ⟩ m ∂t ∥ ∥ D m Ω X α X α q [ ∂⟨δA∥⟩α ( qe∥ ) ⟨ ∂δA ⟩ ] = −m- − v∥--∂t-- + ⟨v⊥ ⋅δE⟩α − v∥e∥ + VD − m-Ω × ∇X ⟨v⋅δA ⟩α ⋅ − δE −-∂t- [ ( ) ⟨ α ⟩ ] ≈ −-q − v∥∂⟨δA∥⟩α + ⟨v⊥ ⋅δE⟩α − v∥e∥ + VD −-qe∥ × ∇X ⟨v⋅δA ⟩α ⋅⟨− δE ⟩α + v∥ ∂A∥- m [ ∂t ( m Ω ) ] ∂t α = −-q ⟨v⊥ ⋅δE⟩α + v∥e∥ + VD − -qe∥ × ∇X ⟨v⋅δA ⟩α ⋅⟨δE⟩α m [ ( m Ω ) ] ≈ −-q ⟨v ⋅δE⟩ + v e + V + v ⟨δB-⊥⟩ ⋅⟨δE ⟩ . (333) m ⊥ α ∥ ∥ D ∥ B0 α
Using Eq. (333) and (), gyrokinetic equation (141) is finally written as
[ ( ) ] -∂ + v∥e∥ + VD + ⟨δE-⟩α ×-e∥-+ v∥ ⟨δB-⊥⟩α ⋅∇X δf ∂t B0 B0 ( ⟨δE-⟩α ×-e∥ ⟨δB-⊥⟩α) = − B0 + v∥ B0 ⋅∇XF0 q [ ( ⟨δB ⟩ ) ] ∂F − -- ⟨v⊥ ⋅δE⟩α + v∥e∥ + VD + v∥---⊥-α- ⋅⟨δE⟩α --0. (334) m B0 ∂ 𝜀

[next] [prev] [prev-tail] [front] [up]