E.2 Expression of δB∥ in terms of δA
Accurate to O(λ1), δB∥ in the above equation is written as (e∥ vector can be considered as constant
because its spatial gradient combined with δA will give O(λ2) terms, which are neglected)
[Using local cylindrical coordinates (r,ϕ,z) with z being along the local direction of B0, and two
components of δA⊥ being δAr and δAϕ, then ∇× δA⊥ is written as
![( ) ( ) [ ]
∂δA-ϕ ∂δAr- 1 ∂-- ∂δAr-
∇ × δA⊥ = − ∂z er + ∂z er + r ∂r(rδAϕ)− ∂ϕ e∥](nonlinear_gyrokinetic_equation320x.png) | (290) |
Note that the parallel gradient operator ∇∥≡ e∥⋅∇ = ∂∕∂z acting on the the perturbed quantities will
result in quantities of order O(λ2). Retaining terms of order up to O(λ), equation (285) is written
as
![[ ]
1 ∂-- ∂-δAr-
∇ ×δA ⊥ ≈ r ∂r(rδAϕ)− ∂ ϕ e∥,](nonlinear_gyrokinetic_equation321x.png) | (291) |
Using this, equation (289) is written as
![[ ]
1 ∂-- ∂δAr-
δB∥ = r ∂r(rδA ϕ)− ∂ϕ .](nonlinear_gyrokinetic_equation322x.png) | (292) |
However, this expression is not useful for GEM because GEM does not use the local coordinates
(r,ϕ,z).]
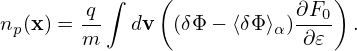
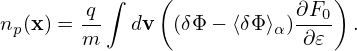
![( ) ( ) [ ]
∂δA-ϕ ∂δAr- 1 ∂-- ∂δAr-
∇ × δA⊥ = − ∂z er + ∂z er + r ∂r(rδAϕ)− ∂ϕ e∥](nonlinear_gyrokinetic_equation320x.png)
![[ ]
1 ∂-- ∂-δAr-
∇ ×δA ⊥ ≈ r ∂r(rδAϕ)− ∂ ϕ e∥,](nonlinear_gyrokinetic_equation321x.png)
![[ ]
1 ∂-- ∂δAr-
δB∥ = r ∂r(rδA ϕ)− ∂ϕ .](nonlinear_gyrokinetic_equation322x.png)