2.4 Distribution function in terms of guiding-center variables

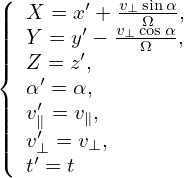
Denote the distribution function expressed in terms of the guiding-center variables (X,𝜀,μ,α) by f_g. Then

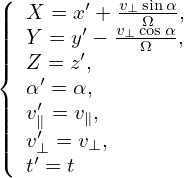(15)

where the value of (x,v) is obtained by the inverse guiding-center transform. Equation (15) along the inverse guiding-center transform can be considered as the definition of f_g.

As is conventionally adopted in multi-variables calculus, both f_p and f_g are sometimes simply denoted by f. Which one is actually assumed depends on the context, i.e., depends on which independent variables are actually assumed: particle variables or guiding-center variables. This is one of the subtle (trivial) things needed to be noted for gyrokinetic theory in particular and for multi-variables calculus in general. It seems better to use subscript notation on f to identify which coordinates are assumed. One example where this distinguishing is important is encountered when we try to express the diamagnetic flow in terms of f_g, which is discussed in Appendix C.

In practice, f_g is often called the guiding-center distribution function whereas f_p is called the particle distribution function. However, they are actually the same distribution function expressed in different variables. The name “guiding-center distribution function” is misleading because it may imply that we can count the number of guiding-centers to obtain this distribution function but this implication is wrong.