[next] [prev] [prev-tail] [tail] [up]

2.5 Spatial gradient operator in guiding-center coordinates

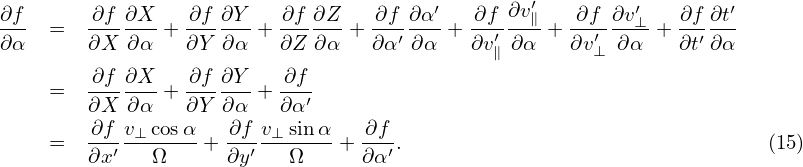
Using the chain-rule, the spatial gradient ∂fp∕∂x is written

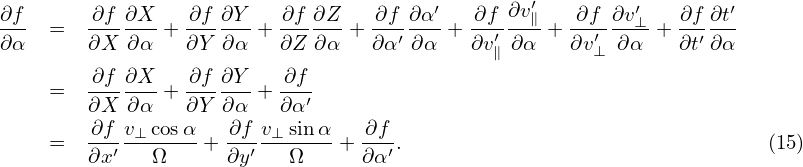∂fp| = ∂X-⋅ ∂fg + ∂𝜀-∂fg+ ∂-μ∂fg + ∂α-∂fg. ∂x v ∂x ∂X ∂x ∂𝜀 ∂x ∂ μ ∂x ∂α
(16)

From the definition of X, Eq. (8), we obtain

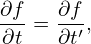∂X ∂ (e∥) -∂x = I+ v × ∂x- Ω- ,
(17)

where I is the unit dyad. From the definition of 𝜀, we obtain

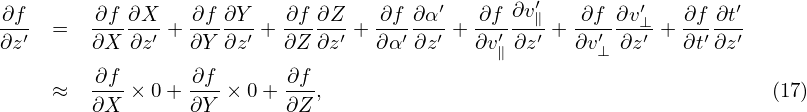∂𝜀 q ---= − --E0, ∂x m
(18)

where E0 = −∂Φ0∕∂x. Using the above results, equation (16) is written as

∂f ∂f [ ∂ (e ) ] ∂f q ∂f ∂μ ∂f ∂α∂f --p |v = --g+ v × --- -∥ ⋅--g − --E0--g + -----g+ ----g . ∂x ∂X ∂x Ω ∂X m ∂𝜀 ∂x ∂μ ∂x ∂α
(19)

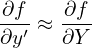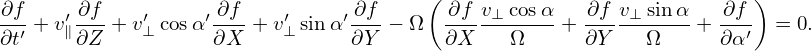As mentioned above, the partial derivative ∂∕∂x is taken by holding v constant. Since B0 is spatially varying, v⊥ is spatially varying when holding v constant. Therefore ∂μ ∂x and ∂α ∂x are generally nonzero. The explicit expressions of these two derivatives are needed later in the derivation of the gyrokinetic equation and is discussed in Appendix G.

For notation ease, define

[ ∂ (e ) ] ∂ λB1 = v × --- -∥ ⋅---, ∂x Ω ∂X
(20)

and

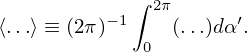∂μ ∂ ∂α ∂ λB2 = -----+ -----, ∂x ∂μ ∂x∂ α
(21)

then expression (19) is written as

∂fp ∂fg q ∂fg ∂x-|v =-∂X + [λB1 + λB2]fg − m-E0 ∂𝜀-.
(22)

[next] [prev] [prev-tail] [front] [up]