[next] [prev] [prev-tail] [tail] [up]

A Adiabatic electron response

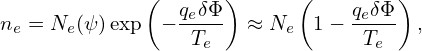
Assume that the total electron density satisfies the Boltzmann distribution on each magnetic surface, i.e.,

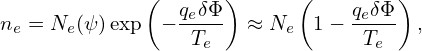( ) ( ) ne = Ne(ψ)exp − qeδΦ- ≈ Ne 1− qeδΦ , Te Te
(285)

where Ne is a radial function. Note that this does not imply that the equilibrium density is Ne (it just implies that the total density is Ne at the location where δΦ = 0, which can still be different from the equilibrium density).

Further assume that the magnetic surface average of δne = ne − ne0 is zero, i.e.,

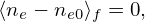⟨ne − ne0⟩f = 0,
(286)

where ne0 is the equilibrium electron density, ⟨…⟩f is the magntic surface averaging operator. Using Eq. (285) in the above condition, we get

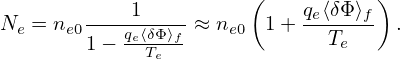1 ( q ⟨δΦ ⟩ ) Ne = ne0----qe⟨δΦ-⟩f-≈ ne0 1 + -e---f- . 1 − --Te--- Te
(287)

Then expression (285) is written as

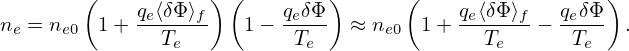( ) ( ) ( ) ne = ne0 1+ qe⟨δΦ⟩f 1− qeδΦ- ≈ ne0 1 + qe⟨δΦ⟩f-− qeδΦ- . Te Te Te Te
(288)

Then the perturbation δne = ne − ne0 is written as

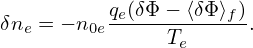δne = − n0eqe(δΦ-−-⟨δΦ⟩f). Te
(289)

This model of electron response is often called adiabatic electron.

A.1 Poisson’s equation with adiabatic electron response

Pluging expression (289) into the Poisson equation (225), we get

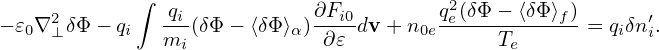∫ 2 -qi ∂Fi0 qe2(δΦ-−-⟨δΦ-⟩f) ′ − 𝜀0∇⊥ δΦ− qi mi (δΦ− ⟨δΦ⟩α) ∂𝜀 dv + n0e Te = qiδn i.
(290)

When solving the Poisson equation, the equation is Fourier expanded in toroidal harmonics and each harmonic is independent of each other, so that they can be solved independently. For n≠0 harmonics, the ⟨δΦ⟩f terms is zero and thus it is trivial to treat the electron term. For the n = 0 harmonic, the ⟨δΦ⟩f term is nonzero and needs special treatment. I use the following method to obtain ⟨δΦ⟩f. First slove the n = 0 harmonic of the following equation:

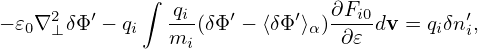∫ 2 ′ -qi ′ ′ ∂Fi0 ′ − 𝜀0∇ ⊥δΦ − qi mi (δΦ − ⟨δΦ ⟩α) ∂𝜀 dv = qiδni,
(291)

(i.e., Eq. (290) with electron term dropped), and then take the magnetic surface average of the solution δΦ′ to get ⟨δΦ′⟩f. It can be proved that ⟨δΦ′⟩f is equal to ⟨δΦ⟩f. Then solving Eq. (290) becomes easier since ⟨δΦ⟩f term is known and can be moved to the right-hand side as a source term.

[next] [prev] [prev-tail] [front] [up]