Velocity gradient operator in guiding-center coordinates

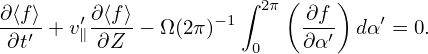
Next, consider the form of the velocity gradient ∂f∕∂v in terms of the guiding-center variables. Using the chain rule, ∂f∕∂v is written

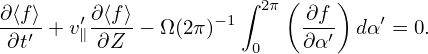∂fp| = ∂X-⋅ ∂fg + ∂𝜀-∂fg+ ∂-μ∂fg + ∂α-∂fg. ∂v x ∂v ∂X ∂v ∂𝜀 ∂v ∂ μ ∂v ∂α

(23)

From the deﬁnition of X, we obtain

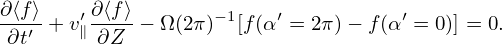
∂X ∂ (v × e ) ---= --- -----∥ ∂v ∂v Ω = ∂v-× e∥ ∂v Ω = I × e∥. (24) Ω

From the deﬁnition of 𝜀, we obtain

∂ 𝜀 ∂v-= v,

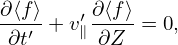(25)

From the deﬁnition of μ, we obtain

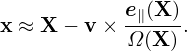∂-μ = v⊥, ∂v B0

(26)

From the deﬁnition of α, we obtain

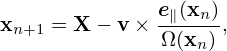∂α 1 ( v⊥) eα ∂v-= v-- e∥ × v-- = v-, ⊥ ⊥ ⊥

(27)

where e_α is deﬁned by

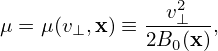v⊥ eα = e∥ × v⊥.

(28)

Using the above results, expression (23) is written

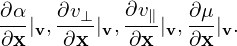∂fp I× e∥ ∂fg ∂fg v⊥ ∂fg eα ∂fg ∂v-|x = --Ω---⋅∂X- + v∂-𝜀 + B0-∂μ-+ v⊥-∂α-.

(29)