[next] [prev] [prev-tail] [tail] [up]

2.7 Time derivatives in guiding-center coordinates

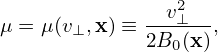
In terms of the guiding-center variables, the time partial derivative ∂fp∕∂t appearing in Vlasov equation is written as

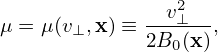∂f ∂f ∂X ∂f ∂V ∂f --p|x,v = --g|X,V + ---⋅--g + ---⋅---g, ∂t ∂t ∂t ∂X ∂t ∂V
(30)

where V = (𝜀,μ,α). Here ∂X∕∂t and ∂V∕∂t are not necessarily zero because the equilibrium quantities involved in the definition of the guiding-center transformation are in general time dependent. This time dependence is assumed to be very slow in the gyrokinetic ordering discussed later. In the following, ∂X∕∂t and ∂V∕∂t will be dropped, i.e.,

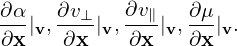∂fp ∂fg ∂t- ≈ ∂t-.
(31)

[next] [prev] [prev-tail] [front] [up]