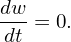
As mentioned in Sec. ??, marker’s weight, w = f∕g, is composed of two factors, namely the physical distribution function f and the markers’ distribution function g. The time evolution of the weight w is thus determined by the time evolution of f and g.. In some cases, the formula for the time evolution of both f and g can be obtained analytically, as discussed in Sec. 4.1 and 4.2, respectively. [*check**In other cases, the formula for the time evolution of f and/or g can not be easily obtained but the formula for the time evolution of w can still be obtained analytically. A typical example of this kind is the full-f simulation including the collision effects in the orbits. In this case, the phase-space flow is not volume-conserving, i.e., dg∕dt≠0, and it is difficult to find an analytic formula for the time evolution of g. However, the conservation of the particle number along the orbits in the phase space is still valid (check this!, wrong), i.e.,
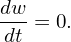 | (72) |
Does this algorithm correctly describe the “collision”? This algorithm (i.e., including the collision effects via randomly changing the orbit variables) is obviously correct when w is 1, i.e., a marker only represents one physical particle. The correctness for wj > 1 case should be verified. ***check]. Collisions in both full-f and δf methods seem to be implemented by including a source term in the evolution equation for the weight, rather than kicking the orbit (I will check the kicking orbit method later).