[next] [prev] [prev-tail] [tail] [up]

5.3 Equilibrium state

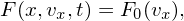
Consider a spatially uniform distribution function given by

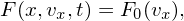F(x,vx,t) = F0(vx),
(80)

where F0(vx) is a known velocity distribution function with number density being equal to those of ions, i.e., ∫ −∞+∞F0(vx)dvx = nion. Consider a case with zero electric field, i.e.,

E (x,t) = 0.
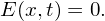(81)

Then it is ready to verify that expression specified by Eqs. (80) and (81) is a equilibrium solution to Vlasov-Poisson system (Eqs. (75) and (79)).

In this note, two kind of equilibrium distribution functions will be considered. The first one is the Maxwellian distribution given by

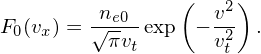ne0 ( v2) F0(vx) = √πv-exp − v2 . t t
(82)

In this system, small perturbation will be damped by a mechanism known as Landau damping. The second kind of distribution considered is the two-stream Maxwellian distribution given by

[ ( 2) ( 2) ] F0(vx) = √ne0-1 exp − (v−-v2b)- + exp − (v-+2vb)-- . πvt2 vt vt
(83)

In this system, small perturbation will give rise to an instability known as the two-stream instability.

[next] [prev] [prev-tail] [front] [up]