[next] [prev] [prev-tail] [tail] [up]

5.4 δf evolution

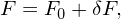
Write the distribution function F as

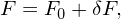F = F0 + δF,
(84)

where F0 is the equilibrium distribution function. Then Eq. (78) is written as

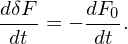dδF- = − dF0-. dt dt
(85)

Use the definition of the orbit propagator,

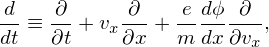d ∂ ∂ edϕ ∂ --≡ --+ vx---+ --------, dt ∂t ∂x m dx ∂vx
(86)

to rewrite the right-hand side of Eq. (85), yielding

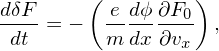( ) dδF-= − e-dϕ-∂F0- , dt m dx ∂vx
(87)

which can be integrated to obtain the time evolution of δF.

The time evolution of δF can also be obtained by using

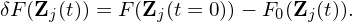δF(Zj(t)) = F(Zj(t = 0))− F0(Zj(t)).
(88)

In this way, the time integration of δF∕dt is avoided, which may reduce the computational work load and improve the accuracy of δF. This seemingly trivial method was emphasized in a CPC paper[1], which introduces an adaptive F0 method based on this idea. I have compared the results of Landau damping obtained by the two methods (i.e., using Eq. (87) and Eq. (88), respectively), which shows they agree with each other very well.

[next] [prev] [prev-tail] [front] [up]