5.5 Normalization

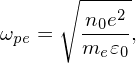
Choose a typical number density n₀ and a typical velocity v₀, then define the electron plasma frequency ω_pe and the Debye length λ_D as

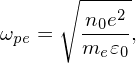(89)

and

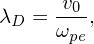(90)

respectively. Using ω_pe and λ_D, define the following normalized quantities:

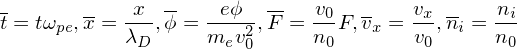(91)

In terms of these normalized quantities, equation (78) is written

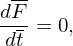(92)

and the Poisson equation (79) is written

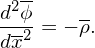(93)

where ρ = n_ion −∫ _−∞^∞Fdv_x.

The equations for the characteristic lines, Eq. (76) and (77), are written

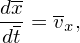(94)

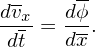(95)

The electric field is given by E = −dϕ∕dx, which, in terms of normalized quantities, is written

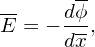(96)

where E = Eeλ_D∕(mv₀²).

In terms of the normalized quantities, the evolution equation (87) of δF is written as

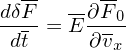(97)

In terms of δF, Poisson’s equation is written as

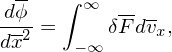(98)

where n_ion = n_e0 has been assumed.