[next] [prev] [prev-tail] [tail] [up]

3.6 Monte-Carlo integration in phase-space

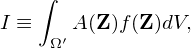
Consider a general integration of the distribution function f in the phase-space

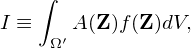∫ I ≡ A(Z )f(Z)dV, Ω′
(53)

where Ω′ is a sub-region of the phase space Ω, A(Z) is a general function of the phase-space coordinates Z, dV is the phase space volume element. As is discussed above, in particle methods, f(Z) is approximated by

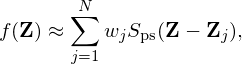N∑ f(Z) ≈ wjSps(Z − Zj), j=1
(54)

where Sps(Z−Zj) is the phase space shape function of markers, N is the total number of marker loaded in the phase space Ω. Using this, expression (53) is written as

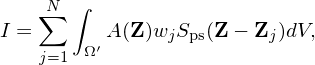N ∫ I = ∑ A (Z)wjSps(Z − Zj)dV, j=1 Ω ′
(55)

If the shape function Sps is chosen to be the Dirac delta function, then the above equation is written as

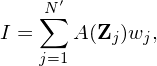′ N∑ I = A(Zj)wj, j=1
(56)

where N′ is the number of markers that are within the sub-region Ω′. Equation (56) is the Monte-Carlo approximation to the integration in Eq. (53)[4, 2].

In PIC simulations, we are usually interested in velocity moments of f averaged in a cell, i.e., A in Eq. (55) is only a function of only v and the velocity integration is over the whole velocity space, whereas the spatial integration is over a small spatial cell. Furthermore, in PIC simulations, the markers are assumed to have a finite shape in the real space (the shape in velocity space is still the Dirac delta function). In this case, Eq. (55) is written as

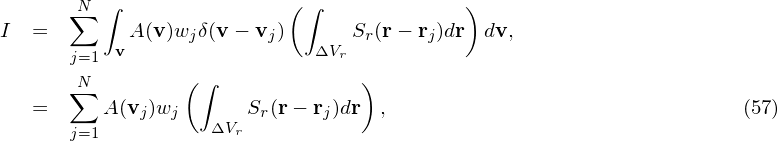
∑N ∫ (∫ ) I = A (v)wjδ(v − vj) Sr(r − rj)dr dv, j=1 v ΔVr ∑N ( ∫ ) = A(vj)wj Sr(r− rj)dr , (57) j=1 ΔVr
where Sr is the shape function. Then the cell-averaged value is written as
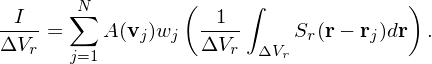-I-- ∑N ( -1--∫ ) ΔVr = A(vj)wj ΔVr ΔV Sr(r − rj)dr . j=1 r
(58)

[next] [prev] [prev-tail] [front] [up]