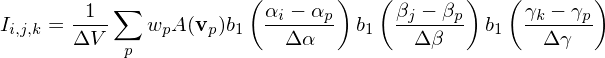
Most PIC codes use the l = 0 b-spline function (i.e., b0, the flat-top function) as the shape function of markers. This model is often called Could in Cell (CIC) since a particle looks like a finite-sized cloud rather than a point. In this case, the cell average of I given in Eq. (43) is written as
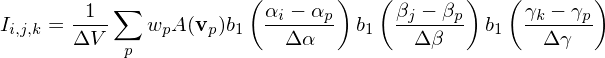 | (51) |
and the electric field on the marker given in Eq. (49) is written as
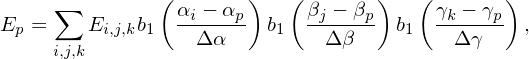 | (52) |
Because the function b1 has a narrow support, as shown in Fig. 1, in practice of calculating Ii,j,k in expression (51), we loop over each particle for only once and assign the contribution of each one to their neighbouring cells (rather than looping over all particle for each cell as the straightforward reading of expression (51) would suggest). The operation of the latter would be O(N × Np), where N is number of grids and Np is the number of markers, while the former is only O(nNp), where n is the number of operation involved in assigning each particle to its neighbouring cells, which is usually much smaller than the grid number N.
Similarly, in calculating the force on a marker, the summation over all the grids (as the straightforward reading of expression (52) would suggest) is not needed. We only need to find which cell a marker is in and then sum the contribution from the nearby grids (rather than all the grids).