Next: Curl operator in general Up: Curvilinear coordinate system Previous: Divergence operator in general
Using the transformation between the two kinds of basis vectors given in Eq.
(152), the gradient of ![]() can be written as
can be written as
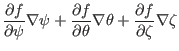 |
|||
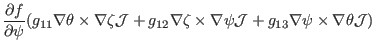 |
|||
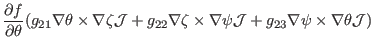 |
|||
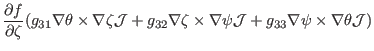 |
|||
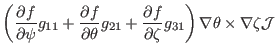 |
|||
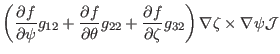 |
|||
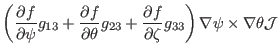 |
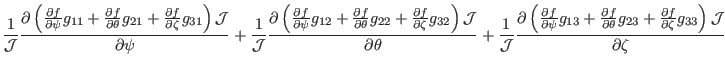 |
|||
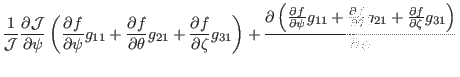 |
|||
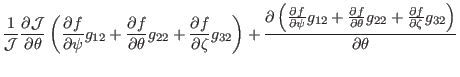 |
|||
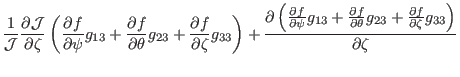 |
(wrong! The derivative of the equilibrium quantities are of order ![]() and thus every term involves these derivatives are of higher order and can be
dropped. Then the above expression reduces to
and thus every term involves these derivatives are of higher order and can be
dropped. Then the above expression reduces to
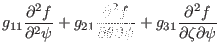 |
|||
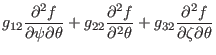 |
|||
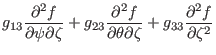 |
(137) |
In field aligned coordinates, and
![]() ,
,
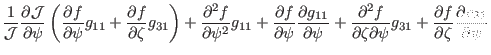 |
(138) | ||
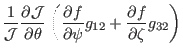 |
|||
 |
|||
yj 2018-03-09