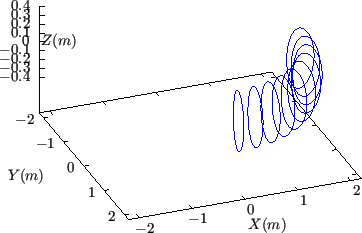
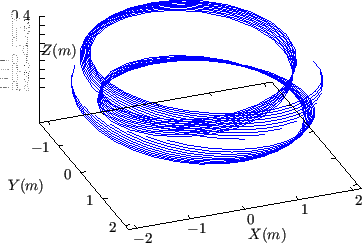
Figure 19 compares a small number of 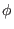 contours and
contours and
 contours on a magnetic surface.
contours on a magnetic surface.
Figure 19:
Comparison between a series of 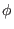 contours
(left) and a series of
contours
(left) and a series of  contours (right) on a magnetic surface. Here
the values of
contours (right) on a magnetic surface. Here
the values of 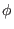 are
are
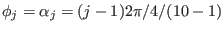 with
with
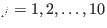 , i.e., only
, i.e., only 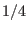 of the full torus. The
values of
of the full torus. The
values of  contours are
contours are
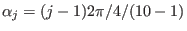 with
with
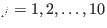 , i.e., only
, i.e., only 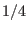 of the full range
of the full range 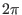 .
Every
.
Every 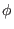 and
and  contours start from the lower-field-side midplane
and go one full poloidal loop. Magnetic field from EAST discharge
#59954@3.03s.
contours start from the lower-field-side midplane
and go one full poloidal loop. Magnetic field from EAST discharge
#59954@3.03s.
 |
As is shown in the left panel of Fig. 19, with 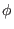 fixed, an
fixed, an
 curve reaches its starting point when
curve reaches its starting point when  changes from zero to
changes from zero to
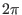 . However, as shown in the right panel of Fig. 19, with
. However, as shown in the right panel of Fig. 19, with
 fixed, an
fixed, an  curve (i.e. a magnetic field line) does not reach
its starting point when
curve (i.e. a magnetic field line) does not reach
its starting point when  changes from zero to
changes from zero to 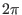 . There is a
toroidal shift,
. There is a
toroidal shift, 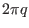 , between the starting point and ending point.
Therefore there is generally no periodic condition along
, between the starting point and ending point.
Therefore there is generally no periodic condition along  since
since 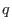 is
not always an integer. A mixed periodic condition involves both
is
not always an integer. A mixed periodic condition involves both  and
and
 is given in (290).
is given in (290).
In field-line-following coordinates
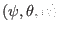 , a toroidal
harmonic of a physical perturbation can be written as
, a toroidal
harmonic of a physical perturbation can be written as
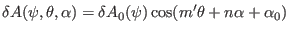 |
(292) |
where 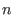 is the toroidal mode number,
is the toroidal mode number, 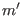 , which may not be an integer, is
introduced to describle the variation along a field line. The periodic
condition given by Eq. (290) requires that
, which may not be an integer, is
introduced to describle the variation along a field line. The periodic
condition given by Eq. (290) requires that
![$\displaystyle \cos (m' \theta + n \alpha + \alpha_0) = \cos [m' (\theta + 2 \pi) + n (\alpha - 2 \pi q) + \alpha_0],$](img940.png) |
(293) |
To satisfy the above condition, we can choose
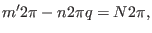 |
(294) |
where 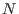 is an arbitrary integer, i.e.,
is an arbitrary integer, i.e.,
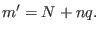 |
(295) |
We are interested in perturbation with a slow variation along the field line
direction (i.e., along
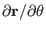 ) and thus we
want the value of
) and thus we
want the value of 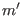 to be small. One of the possible small values given by
expression (295) is
to be small. One of the possible small values given by
expression (295) is
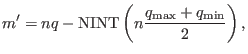 |
(296) |
where N
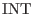 is a function that return the nearest integer of its
argument,
is a function that return the nearest integer of its
argument, 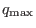 and
and 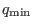 is the maximal and minimal value of the
safety factor in the radial region in which we are interested. Note that
is the maximal and minimal value of the
safety factor in the radial region in which we are interested. Note that 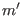 depends on the radial coordinate
depends on the radial coordinate 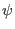 through
through 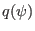 . Also note that
. Also note that
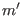 here is differnt from the poloidal mode number
here is differnt from the poloidal mode number 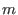 in
in
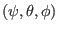 coordinate system. It is ready to show that the perturbation given by
Eq. (292) with
coordinate system. It is ready to show that the perturbation given by
Eq. (292) with 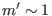 and
and 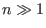 has large poloidal mode
number
has large poloidal mode
number 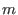 when expressed in
when expressed in
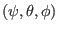 coordinates. [Proof:
Expression (292) can be written as
coordinates. [Proof:
Expression (292) can be written as
![$\displaystyle \delta A = \delta A_0 (\psi) \cos [m' \theta + n (\phi - \overline{\delta} (\psi, \theta)) + \alpha_0]$](img952.png) |
(297) |
If  is the staight-field-line poloidal angle in
is the staight-field-line poloidal angle in
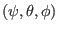 coordinate system, then
coordinate system, then
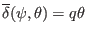 and the
above eqaution is written as
and the
above eqaution is written as
which indicates the poloidal mode number 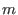 in
in
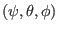 coordinates is given by
coordinates is given by
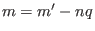 . For the case with
. For the case with 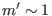 and
and 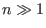 ,
, 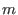 is much larger than one.]
is much larger than one.]
[In the past, I choose
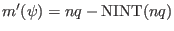 . However,
. However, 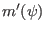 in this case is not a continuous function of
in this case is not a continuous function of 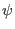 and thus is not
physical.]
and thus is not
physical.]
[In passing, let us introduce the binormal wavenumber, which is frequently
used in presenting turbulence simulation results. Consider the toroidal phase
in expression (292), i.e.,
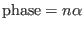 |
(298) |
Define the binormal direction
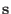 by
by
which a unit vector lying on a magnetic surface and perpendicular to
 . The binormal wavenumber is defined by
. The binormal wavenumber is defined by
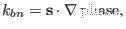 |
(299) |
which can be written as
Using
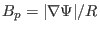 , the above equation is written
, the above equation is written
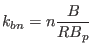 |
(301) |
which indicates the binormal wavenumber generally depends on the poloidal
angle. For large aspect-ratio tokamak, we have
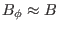 ,
,
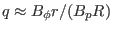 . Then Eq. (301) is written
. Then Eq. (301) is written
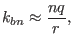 |
(302) |
which indicates the binormal wavenumber are approximately indepenent of the
poloidal angle. For modes with field aligned structure (i.e.,
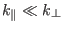 ), we have
), we have
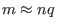 , where
, where 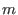 is the poloidal mode numer
along
is the poloidal mode numer
along  with
with 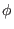 hold fixed. In this case, the above equation is
written
hold fixed. In this case, the above equation is
written
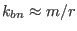 , which is the usual poloidal wave number. Due
to this relation, the binormal wavenumber
, which is the usual poloidal wave number. Due
to this relation, the binormal wavenumber 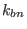 is often denoted by
is often denoted by
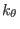 in papers on tokamak turbulence. In some papers the binormal
wavenumber is denoted by
in papers on tokamak turbulence. In some papers the binormal
wavenumber is denoted by 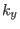 .]
.]
Since  contours are magnetic field lines, they span out the 3D shape
of the magnetic surface when there are enough numbe of
contours are magnetic field lines, they span out the 3D shape
of the magnetic surface when there are enough numbe of  contours on a
magnetic surface, as is shown by the left-panel of Fig. 20.
contours on a
magnetic surface, as is shown by the left-panel of Fig. 20.
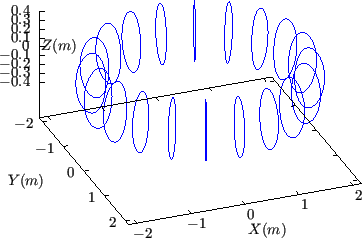
Figure 20:
Comparison between a series of 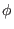 contours(left) and a series of
contours(left) and a series of  contours (left) on a magnetic
surface. The
contours (left) on a magnetic
surface. The  contours correspond to magnetic field lines. Here the
contours correspond to magnetic field lines. Here the
 values of adjacent
values of adjacent  contours differ by
contours differ by
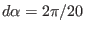 and each
and each  contour goes one full poloidal loop. Magnetic field
from EAST discharge #59954@3.03s.
contour goes one full poloidal loop. Magnetic field
from EAST discharge #59954@3.03s.
 |
yj
2018-03-09
![]() contours and
contours and
![]() contours on a magnetic surface.
contours on a magnetic surface.


![]() fixed, an
fixed, an
![]() curve reaches its starting point when
curve reaches its starting point when ![]() changes from zero to
changes from zero to
![]() . However, as shown in the right panel of Fig. 19, with
. However, as shown in the right panel of Fig. 19, with
![]() fixed, an
fixed, an ![]() curve (i.e. a magnetic field line) does not reach
its starting point when
curve (i.e. a magnetic field line) does not reach
its starting point when ![]() changes from zero to
changes from zero to ![]() . There is a
toroidal shift,
. There is a
toroidal shift, ![]() , between the starting point and ending point.
Therefore there is generally no periodic condition along
, between the starting point and ending point.
Therefore there is generally no periodic condition along ![]() since
since ![]() is
not always an integer. A mixed periodic condition involves both
is
not always an integer. A mixed periodic condition involves both ![]() and
and
![]() is given in (290).
is given in (290).
![]() , a toroidal
harmonic of a physical perturbation can be written as
, a toroidal
harmonic of a physical perturbation can be written as
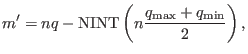
![]() . However,
. However, ![]() in this case is not a continuous function of
in this case is not a continuous function of ![]() and thus is not
physical.]
and thus is not
physical.]
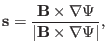
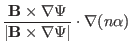
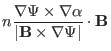
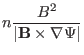
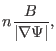
![]() contours are magnetic field lines, they span out the 3D shape
of the magnetic surface when there are enough numbe of
contours are magnetic field lines, they span out the 3D shape
of the magnetic surface when there are enough numbe of ![]() contours on a
magnetic surface, as is shown by the left-panel of Fig. 20.
contours on a
magnetic surface, as is shown by the left-panel of Fig. 20.

