Constructing model tokamak magnetic ﬁeld

10 Constructing model tokamak magnetic ﬁeld

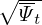
In some cases (e.g., turbulence simulation), model tokamak magnetic ﬁeld, which is not an exact solution to the GS equation, is often used. In the model, the safety factor proﬁle q(ψ), toroidal ﬁeld function g(ψ), and the magnetic surface shape (R(ψ,𝜃),Z(ψ,𝜃)) are given. To use this model in a simulation, we need to calculate its poloidal magnetic ﬁeld, which is determined by the poloidal magnetic ﬂux function Ψ. To determine Ψ, we need to use Eq. (160), i.e.,

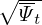∫ 2π q(ψ) = −-1-g- 𝒥-d𝜃, 2π Ψ′ 0 R2

(219)

and re-organize the formula as

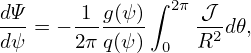dΨ 1 g(ψ )∫ 2π 𝒥 ---= − ------- --2d𝜃, dψ 2π q(ψ ) 0 R

(220)

which can be integrated to obtain Ψ and thus the poloidal magnetic ﬁeld B_p = ∇Ψ ×∇ϕ, where 𝒥 = [(∇ψ ×∇𝜃) ⋅∇ϕ]⁻¹. The toroidal magnetic ﬁeld can be obtained from g(ψ) by B_ϕ = g∕R. In most papers, g(ψ) is chosen to be a constant.

A typical magnetic surface shape used in simulations is the Miller shape, which is given by

R (r,𝜃) = R0 (r)+ r cos[𝜃+ (sin−1δ(r))sin𝜃] Z (r,𝜃) = κ(r)rsin 𝜃

(221)

where r = ψ is the radial coordinate, R₀(r), δ(r), and κ_r(r) are the Shafronov shift, triangularity, and elongation proﬁles, which can be arbitrarily speciﬁed. For the special case of R₀ being a constant, δ(r) = 0, and κ(r) = 1, this shape reduces to a concentric-circular magnetic ﬁeld. An example of calculating the poloidal ﬁeld of the model ﬁeld is given in Sec. 14. This kind of model ﬁeld can be called theoretical physicists’ tokamak. Computational physicists often use this model for code benchmarking purpose. The famous DIII-D cyclone base case is an example, which was extensively used for benchmarking gyrokinetic simulation of ion temperature driven turbulence.

[next] [prev] [prev-tail] [front] [up]