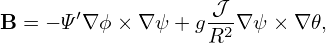
A coordinate system (ψ,𝜃,ϕ), where ϕ is the usual cylindrical toroidal angle, is called a magnetic surface coordinate system if Ψ is a function of only ψ, i.e., ∂Ψ∕∂𝜃 = 0 (we also have ∂Ψ∕∂ϕ = 0 since we are considering axially symmetrical case). In terms of (ψ,𝜃,ϕ) coordinates, the contravariant form of the magnetic field, Eq. (149), is written as
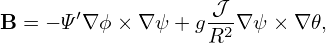 | (153) |
where Ψ′≡ dΨ∕dψ. The covariant form of the magnetic field, Eq. (150), is written as
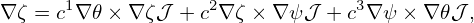 | (154) |