[next] [tail] [up]

1.1 Poloidal magnetic field

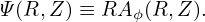
Equation (3) indicates that the two poloidal components of B, namely BR and BZ, are determined by a single component of A, namely Aϕ. This motivates us to define a function Ψ(R,Z):

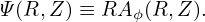Ψ (R, Z) ≡ RA (R,Z ). ϕ
(4)

Then Eq. (3) implies the poloidal components, BR and BZ, can be written as

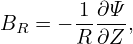-1∂-Ψ BR = −R ∂Z ,
(5)

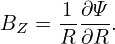1 ∂Ψ BZ = ----. R ∂R
(6)

(Note that it is the property of being axisymmetric and divergence-free that enables us to express the two components of B, namely BR and BZ, in terms of a single function Ψ(R,Z).) Furthermore, it is ready to prove that Ψ is constant along a magnetic field line, i.e. B ⋅∇Ψ = 0. [Proof:

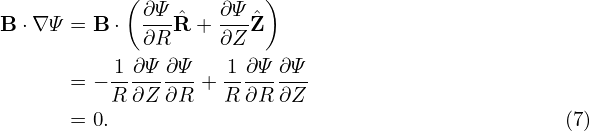
( ∂Ψ ∂Ψ ) B ⋅∇ Ψ = B ⋅ ∂RRˆ+ ∂ZZˆ = − 1-∂Ψ-∂Ψ-+ 1-∂Ψ-∂Ψ- R ∂Z ∂R R ∂R ∂Z = 0. (7)
]

The function Ψ is usually called the “poloidal flux function” in tokamak literature because Ψ can be related to the poloidal magnetic flux, as we will discuss in Sec. 1.7.

Using Eqs. (5) and (6), the poloidal magnetic field Bp is written as

ˆ ˆ Bp = BRR +BZ Z = −-1∂-ΨRˆ+ -1∂Ψ-ˆZ R ∂Z R ∂R = 1-∇Ψ × ˆϕ R = ∇Ψ × ∇ ϕ (8)

[next] [front] [up]