Relation of Ψ with the poloidal magnetic ﬂux

1.7 Relation of Ψ with the poloidal magnetic ﬂux

Note that Ψ is deﬁned by Ψ = RA_ϕ, which is just a component of the vector potential A, thereby having no obvious physical meaning. Next, we try to ﬁnd the physical meaning of Ψ, i.e., try to ﬁnd some simple algebraic relation of Ψ with some quantity that can be measured in experiments.

pict

Fig. 2: The poloidal magnetic ﬂux Ψ_p between the two magnetic surfaces Ψ₁ and Ψ₂ is given by Ψ_p = 2π(Ψ₂ − Ψ₁).

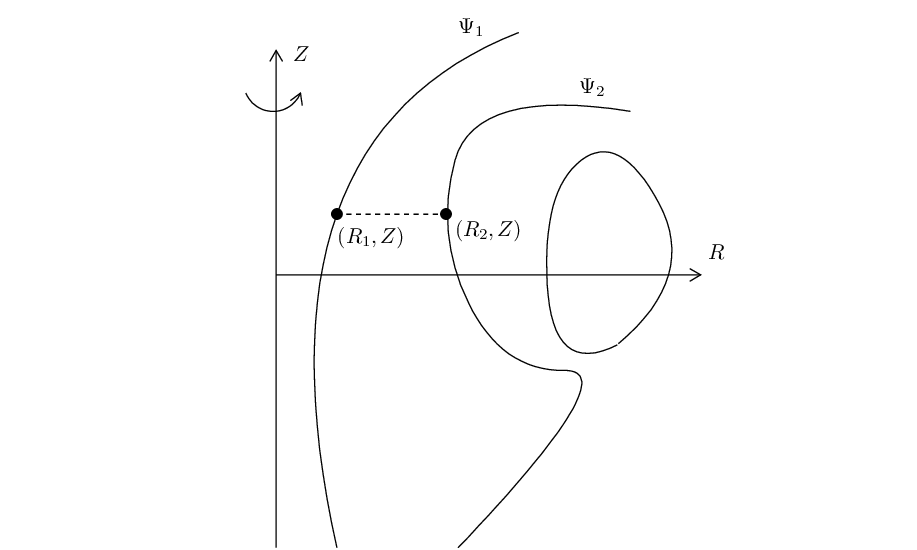
In Fig. 2, there are two magnetic surfaces labeled, respectively, by Ψ = Ψ₁ and Ψ = Ψ₂. Using Gauss’s theorem in the toroidal volume between the two magnetic surface, we know that the poloidal magnetic ﬂux through any toroidal ribbons between the two magnetic surfaces is equal to each other. Next, we calculate this poloidal magnetic ﬂux. To make the calculation easy, we select a plane perpendicular to the Z axis, as is shown by the dash line in Fig. 1. In this case, only B_Z contribute to the poloidal magnetic ﬂux, which is written (the positive direction of the plane is chosen in the direction of )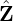

∫ R2 Ψp = R1 Bz (R, Z)2πRdR ∫ R2 = -1∂-Ψ2πRdR R1∫ R ∂R R2 ∂Ψ- = 2π R1 ∂R dR = 2π[Ψ − Ψ ]. (20) 2 1

Equation (20) provides a simple physical meaning for Ψ, i.e., the diﬀerence of 2πΨ between two magnetic surfaces is equal to the poloidal magnetic ﬂux enclosed by the two magnetic surfaces. Noting that we are considering the axisymmetric case, the physical meaning of Ψ can also be stated as: the diﬀerence of Ψ between two magnetic surfaces is equal to the poloidal magnetic ﬂux per radian. Due to this relation, Ψ is usually called the “poloidal magnetic ﬂux function” in tokamak literature. Note that it is the diﬀerence of Ψ between two locations that determines the the physical quantities Ψ_p, which is consistent with the fact that gauge transformation (14) dose not change the values of physical quantities.

[next] [prev] [prev-tail] [front] [up]