Due to the divergence-free nature of magnetic field, i.e., ∇⋅ B = 0, magnetic field can be expressed as the curl of a vector field,
|
| (1) |
where A is called the vector potential of B. (Using a vector potential representation is helpful in that we do not need to worry about the condition ∇⋅B = 0 once the magnetic field is in the vector potential form.)
In cylindrical coordinates (R,ϕ,Z), the above expression is written
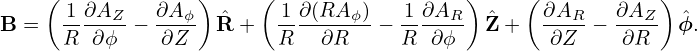 | (2) |
We consider axisymmetric magnetic field. The axial symmetry means that, when expressed in the cylindrical coordinate system (R,ϕ,Z), the components of B, namely BR, BZ, and Bϕ, are all independent of ϕ. For this case, it can be proved that an axisymmetric vector potential A suffices for expressing the magnetic field, i.e., all the components of the vector potential A can also be taken independent of ϕ. Using this, Eq. (2) is written
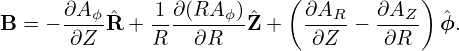 | (3) |
In tokamak literature,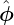 
direction is called the toroidal direction, and (R,Z) planes (i.e., ϕ = const
planes) are called poloidal planes.