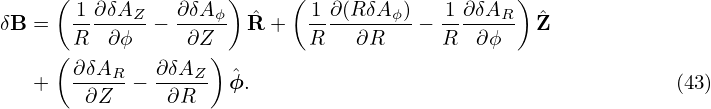
In the above, the magnetic field is assumed to be axisymmetric. With this assumption, the poloidal magnetic field (having two components) can be expressed in terms of a single component of the vector potential A, Aϕ (specifically via Ψ ≡ AϕR). This kind of simplification can not be achieved if the axisymmetricity assumption is dropped, because other components of the vector potential (namely AR and AZ) will appear in the expression of the poloidal magnetic field. Let us re-examine Eq. (2) for a magnetic perturbation:
When studying tearing modes and turbulence, most authors narrow the possible perturbed magnetic field by setting δAR = δAZ = 0, i.e.,
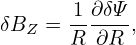 | (44) |
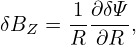 | (45) |
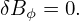 | (46) |
where δΨ = RδAϕ. Therefore this kind of magnetic perturbation can be written in the same form of the equilibrium poloidal magnetic field:
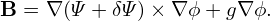 | (47) |
The above approximation is widely used in theory and simulation (e.g., tearing mode theory; turbulence simulation, where δAϕ is replaced by δA∥.) Do we miss some magnetic perturbations that is important for plasma transport when using the above specific form?
The total magnetic field is then written as
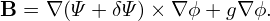 | (48) |
**check**Can the projection of the total magnetic field line in the poloidal plane can be traced by tracing the contour of Ψ + δΨ? No. The contours of Ψ + δΨ will not show island structures in the poloidal plane. To show the expected island structures, we need to subtract non-reconnecting poloidal magnetic field from the total poloidal field. I will discuss this in Sec. (), where I will show that contours of the so-called helical flux will give the expected island structures near the resonant surfaces.**can be worng, I have not checked this.
Next, we return to discuss the 2D case (i.e., assuming axisymmetry).