1.10 Safety factor

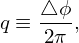
Magnetic field lines on closed magnetic surfaces travel closed curves in a poloidal plane. For these field lines, we can define the safety factor q, which is the number of toroidal loops a magnetic field line travels when it makes one poloidal loop, i.e.

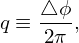(33)

where △ϕ as the change of the toroidal angle when a magnetic field line travels a full poloidal loop. The safety factor can also be understood as the average pitch angle of a magnetic field line in (𝜃,ϕ) plane of a closed magnetic surface.

For open field line region (where a field line touches the wall before its poloidal projection can close itself), the “connection length” is often used to characterize the magnetic field.

Expression of safety factor in terms of magnetic field

The equation of magnetic field lines is given by

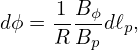(34)

where dℓ_p is the line element along the direction of B_p on the poloidal plane. Equation (34) can be arranged in the form

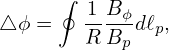(35)

which can be integrated over dℓ_p to give

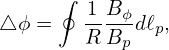(36)

where the line integration is along the poloidal magnetic field (the contour of Ψ on the poloidal plane). Using this, Eq. (33) is written

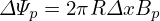(37)

Expression of safety factor in terms of magnetic flux

The safety factor given by Eq. (37) is expressed in terms of the components of the magnetic field. The safety factor can also be expressed in terms of the magnetic flux. Define ΔΨ_p as the poloidal magnetic flux enclosed by two neighboring magnetic surface, then ΔΨ_p is given by

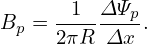(38)

where Δx is the length of a line segment in the poloidal plane between the two magnetic surfaces, which is perpendicular to the first magnetic surface (so perpendicular to the B_p). Note that Δx, as well as R and B_p, generally depends on the poloidal location whereas ΔΨ_p is independent of the poloidal location.

Using Eq. (38), the poloidal magnetic field is written as

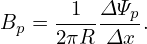(39)

Substituting Eq. (39) into Eq. (37), we obtain

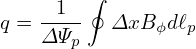(40)

We know ΔΨ_p is a constant independent of the poloidal location, so ΔΨ_p can be taken outside the integration to give

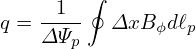(41)

It is ready to realise that the integral appearing in Eq. (41) is the toroidal magnetic flux enclosed by the two magnetic surfaces, ΔΨ_t. Using this, Eq. (41) is written as

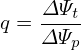(42)

Equation (42) indicates that the safety factor of a magnetic surface is equal to the differential of the toroidal magnetic flux with respect to the poloidal magnetic flux enclosed by the magnetic surface.

Rational surfaces vs. irrational surfaces

If the safety factor of a magnetic surface is a rational number, i.e., q = m∕n, where m and n are integers, then this magnetic surface is called a rational surface, otherwise an irrational surface. A field line on a rational surface with q = m∕n closes itself after it travels n poloidal loops. An example of a field line on a rational surface is shown in Fig. 5.