3.3 Axisymmetric equilibrium magnetic field

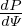
A general axisymmetric magnetic field (which does not necessarily satisfy the force balance), is given by Eq. (10), i.e.,

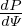(68)

For the above axisymmetric magnetic field to be consistent with the force balance equation (56), there are additional requirements for Ψ and g. Specifically, Ψ is restricted by the GS equation and g should be a function of only Ψ. Therefore an axisymmetric equilibrium magnetic field is fully determined by two functions, Ψ = Ψ(R,Z) and g = g(Ψ). The Ψ is determined by solving the GS equation with specified RHS source terms and boundary conditions.

The RHS source terms in the GS equation (66) are P(Ψ) and g(Ψ), both of which must be specified before the GS equation can be solved. For most cases, the source terms are nonlinear about Ψ and thus the GS equation is a two-dimensional (in R and Z) nonlinear partial differential equation for Ψ.

For most choices of P(Ψ) and g(Ψ), the GS equation (66) has to be solved numerically. For some particular choices of P and g profiles, analytical solutions are available, one of which is the Solovév equilibrium and is discussed in Appendix A.1.

Note that we solve the GS equation in order to obtain the poloidal magnetic flux Ψ and thus the poloidal magnetic field. The toroidal magnetic field must be specified in some way before we can solve the GS equation. There are several ways of specifying the toroidal magnetic field: (1) given g(Ψ), (2) given ⟨j_∥⟩, (3) given the safety factor q(Ψ). There are simple relations between g, ⟨j_∥⟩, and q, which allows translation form one to another (discussed later). In transport simulations, ⟨j_∥⟩ is obtained from current drive models and neoclassical bootstrap current models. Note that the specification of the source terms (P, g, q, and ⟨j_∥⟩) usually involve the unknown Ψ (via not only the explicit presence of Ψ, but also the flux-surface averaging which implicit involves Ψ). This indicates that iterations are needed when numerically solving the GS equation.

Many physical processes in tokamak are sensitive to the magnetic configuration. Serious numerical simulations should use magnetic field that satisfies the Grad-Shafranov equation and, if possible, use realistic magnetic fields reconstructed from experimental data.