[next] [tail] [up]

A.1 Solovév equilibrium

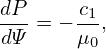
For most choices of P(Ψ) and g(Ψ), the GS equation (66) has to be solved numerically. For the particular choice of P and g profiles given by

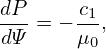dP-= − c1, dΨ μ0
(511)

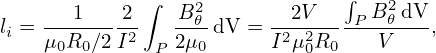dg- 2 g dΨ = − c2R0,
(512)

analytical solution to the GS equation can be found, which is given by[16]

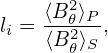1 1 Ψ = -(c2R20 + c0R2)Z2 +-(c1 − c0)(R2 − R20)2, 2 8
(513)

where c0, c1, c2, and R0 are arbitrary constants. [Proof: By direct substitution, we can verify Ψ of this form is indeed a solution to the GS equation (66).] A useful choice for tokamak application is to set c0 = B0∕(R02κ0q0), c1 = B0(κ02 + 1)∕(R02κ0q0), and c2 = 0. Then Eq. (513) is written

[ ] ---B0-- 2 2 κ20 2 22 Ψ = 2R20κ0q0 R Z + 4 (R − R 0) ,
(514)

which can be solved analytically to give the explicit form of the contour of Ψ on (R,Z) plane:

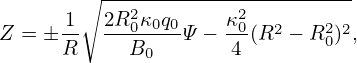∘ ----------------------- 1 2R2κ0q0 κ2 Z = ± -- --0----Ψ − -0(R2 − R20)2, R B0 4
(515)

which indicates the magnetic surfaces are up-down symmetrical. Using Eq. (511), i.e.,

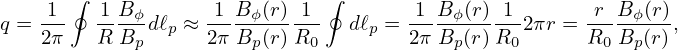dP c1 B0(κ2+ 1) ---= − ---= − ----02----, dΨ μ0 μ0R 0κ0q0
(516)

the pressure is written

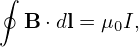2 P = P0 − B0-(κ20 +-1)Ψ, μ0R0κ0q0
(517)

where P0 is a constant of integration. Note Eq. (514) indicates that that Ψ = 0 at the magnetic axis (R = R0,Z = 0). Therefore, Eq. (517) indicates that P0 is the pressure at the magnetic axis. The toroidal field function g is a constant in this case, which implies there is no poloidal current in this equilibrium. (For the Solovev equilibrium (514), I found numerically that the value of the safety factor at the magnetic axis (R = R0,Z = 0) is equal to q0g∕(R0B0). This result should be able to be proved analytically. I will do this later. In calculating the safety factor, we also need the expression of |∇Ψ|, which is given analytically by

∘ (---)----(---)-- ∂-Ψ 2 ∂-Ψ 2 |∇Ψ | = ∂R + ∂Z B ∘ ------------------------------- = ---20-- [2RZ2 + κ20(R2 − R20)R ]2 + (2R2Z )2. (518) 2R 0κ0q0
)

 

Define Ψ0 = B0R02, and Ψ = Ψ∕Ψ0, then Eq. (514) is written as

-- 1 [--2-2 κ2 --2 ] Ψ = ----- R Z + -0(R − 1)2 , (519) 2κ0q0 4
where R = R∕R0, Z = Z∕R0. From Eq. (519), we obtain
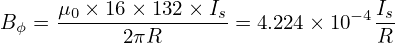∘ ------------------- -- 1 -- κ20 --2 Z = ± R- 2κ0q0Ψ − -4 (R − 1)2.
(520)

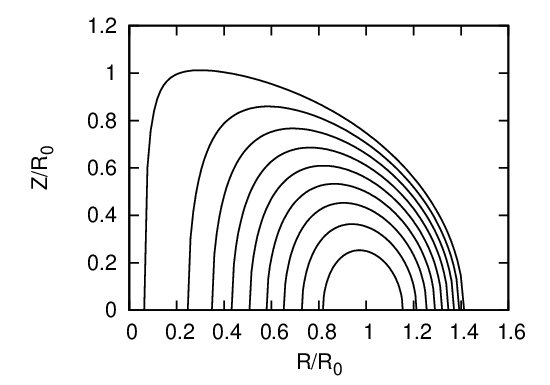
Given the value of κ0, q0, for each value of Ψ, we can plot a magnetic surface on (R,Z) plane. An example of the nested magnetic surfaces is shown in Fig. 38.

pict

Fig. 38: Flux surfaces of Solovév equilibrium for κ0 = 1.5 and q0 = 1.5, with Ψ varying from zero (center) to 0.123 (edge). The value of Ψ on the edge is determined by the requirement that the minimum of R is equal to zero. (To prevent “divided by zero” that appears in Eq. (520) when R = 0, the value of Ψ on the edge is shifted to 0.123 − 𝜀 when plotting the above figure, where 𝜀 is a small number, 𝜀 = 10−3 in this case.)

The minor radius of a magnetic surface of the Solovev equilibrium can be calculated by using Eq. (515), which gives

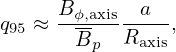∘-----√---- Rin = R20 − AΨ,
(521)

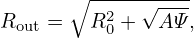∘ -----√---- Rout = R20 + A Ψ,
(522)

and thus

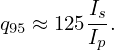∘ ---------- ∘ ---------- R2 + √A-Ψ − R2 − √A-Ψ a = Rout −-Rin =---0-------------0------. 2 2
(523)

where A = 8R02q0∕(B0κ0). In my code of constructing Solovev magnetic surface, the value of a is specified by users, and then Eq. (523) is solved numerically to obtain the value of Ψ of the flux surface. Note that the case Ψ = 0 corresponds to Rin = Rout = R0, i.e., the magnetic axis, while the case Ψ = R02B0κ0∕(8q0) corresponds to Rin = 0. Therefore, the reasonable value of Ψ of a magnetic surface should be in the range 0 ≤ Ψ < R02B0κ0∕(8q0). This range is used as the interval bracketing a root in the bisection root finder.

Using Eq. (523), the inverse aspect ratio of a magnetic surface labeled by Ψ can be approximated as[16]

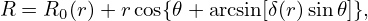∘ -------- 2q0Ψ 𝜀 ≈ κ-R2B--. 0 0 0
(524)

Therefore, the value of Ψ of a magnetic surface with the inverse aspect ratio 𝜀 is approximately given by

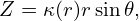𝜀2κ R2B Ψ = ---0-0--0. 2q0
(525)

[next] [front] [up]