Solving by inverting the Laplace operator

4.1 Solving by inverting the Laplace operator

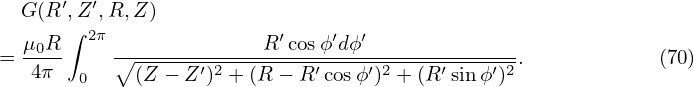
If we want to invert the Laplace operator △^∗ of the GS equation to solve for Ψ, we encounter two issues: (1) the RHS of the GS equation involves functions of Ψ, where both the functions and Ψ are unknown; (2) the values of Ψ on a given boundy should be prescribed, which in turn invovles two issues: (a) how to choose the shape of the bounday? (b) how to know the value of Ψ on the boundary? The answer to isssues (a) and (b) is that we can choose any boundy we like (e.g., rectangular region) and guess the values of Ψ on it (which will be updated in iterations discussed later). The answer to issue (1) is that the function forms are chosen by users, usually as polymials in Ψ, e.g. [?]

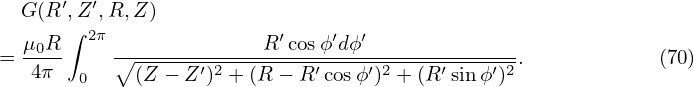dP (Ψ ) ∑np n np+1∑np --dΨ--= αnx − x αn, n=0 n=0

(70)

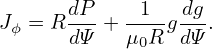dg- n∑g n ng+1 n∑g 2gdΨ = βnx − x βn, n=0 n=0

(71)

where x = (Ψ − Ψ_M)∕(Ψ_B − Ψ_M), Ψ_M and Ψ_B are values of Ψ at the magnetic axis and LCFS (but the locations of the axis and LCFS are unknown), the free parameters α_n and β_n are assumed known (which will be later adjusted in the least-square-minimizing iteration to make the resulting solution match some measurements and constraints imposed). To make the RHS fully known, we need to guess values of Ψ in the inner region. Then inverting △^∗ to get new Ψ. The values we obtained via inerting △^∗ usually diﬀer from what we used in the RHS, so we need to interate until convergence. We call this interation as the ﬁrst-level iteration.

After the ﬁrst-level iteration coverges, we can calculate J_ϕ through Eq. (67) or Eq. (54). After this, all the current (current in the plasma, and current in the external coils, which are assumed to be known) perpendicular to the poloidal plane is known, we can calculate the value of Ψ on the boundary, Ψ_b, by using the Biot-Savart Law (see (641)):

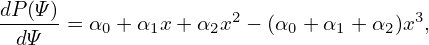∫ ∑Nc Ψ(R,Z ) = G(R′,Z′;R, Z)JϕdR′dZ′ + G (Rci,Zci;R,Z)Ici,ϕ, P i=1

(72)

where G is Green’s function given by

G (R ′,Z ′,R,Z ) μ R ∫ 2π R ′cosϕ ′dϕ′ = --0- ∘-------′2--------′----′2-----′---′2- (73) 4π 0 (Z − Z ) + (R − R cosϕ) + (R sinϕ )

If Ψ_b calculated this way diﬀers from the initial guess of the value of Ψ on the boundary, we need to iterate: use the Ψ_b calculated as a new guess value of Ψ on the boundary and repeat the above procedures until convergence. We call this iteration as the second-level iteration.[?].

The thrid level iteration is to iterate over the free parameters α_n, β_n, the PF coil currents, to make the solution match match some measurements and constraints imposed. This iteration is an optimization problem.

[next] [front] [up]