Gradient and directional derivative in general coordinates (ψ,𝜃,ζ)

6.5 Gradient and directional derivative in general coordinates (ψ,𝜃,ζ)

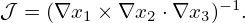
The gradient of a scalar function f(ψ,𝜃,ζ) is readily calculated from the chain rule,

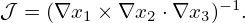∇f = ∂f∇ ψ + ∂f∇ 𝜃+ ∂f-∇ζ. ∂ψ ∂𝜃 ∂ ζ

(102)

Note that the gradient of a scalar function is in the covariant representation. The inverse form of this expression is obtained by dotting the above equation respectively by the three contravariant basis vectors, yielding

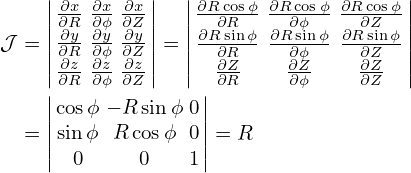∂f ∂r ∂ψ-= (𝒥 ∇𝜃 ×∇ ζ)⋅∇f = ∂ψ-⋅∇f

(103)

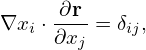∂f ∂r ---= (𝒥 ∇ζ ×∇ ψ)⋅∇f = ---⋅∇f ∂𝜃 ∂𝜃

(104)

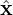∂f ∂r ∂ζ-= (𝒥 ∇ψ × ∇𝜃)⋅∇f = ∂ζ-⋅∇f

(105)

Using Eq. (102), the directional derivative in the direction of ∇ψ is written as

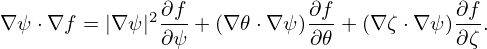∂f ∂f ∂f ∇ ψ ⋅∇f = |∇ ψ|2∂ψ-+ (∇𝜃 ⋅∇ψ)-∂𝜃 + (∇ ζ ⋅∇ ψ)∂ζ.

(106)

[next] [prev] [prev-tail] [front] [up]