Divergence operator in general coordinates (ψ,𝜃,ζ)

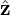
To calculate the divergence of a vector, it is desired that the vector should be in the contravariant form because we can make use of the fact:

∇ ⋅(∇ α× ∇ β) = 0,

(107)

for any scalar quantities α and β. Therefore we write vector A as

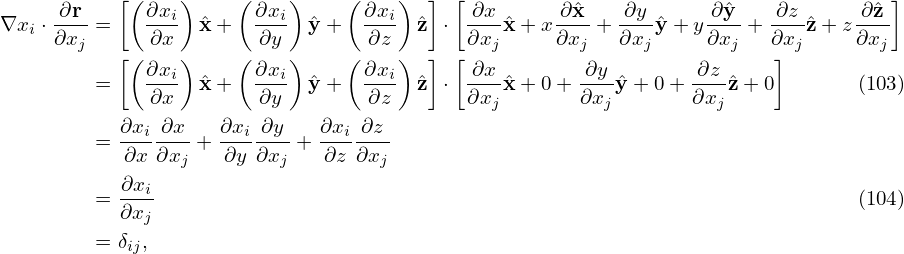A = A(ψ)𝒥∇ 𝜃× ∇ ζ + A(𝜃)𝒥 ∇ ζ × ∇ ψ+ A (ζ)𝒥∇ ψ × ∇𝜃,

(108)

where A^(ψ) = A ⋅∇ψ, A^(𝜃) = A ⋅∇𝜃, A^(ζ) = A ⋅∇ζ. Then the divergence of A is readily calculated as

(ψ) (𝜃) (ζ) ∇ ⋅A = (∇ 𝜃(× ∇ ζ)⋅∇ (A 𝒥 )+ (∇ ζ × ∇ ψ))⋅∇ (A 𝒥 )+ (∇ψ × ∇𝜃) ⋅∇(A 𝒥 ) (109) = 1- ∂A(ψ)𝒥-+ ∂A-(𝜃)𝒥-+ ∂A-(ζ)𝒥- , (110) 𝒥 ∂ψ ∂𝜃 ∂ζ

where the second equality is obtained by using Eqs. (103), (104), and (105).