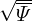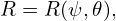
Metric elements of the (ψ,𝜃,ϕ) coordinates, e.g., ∇ψ ⋅∇𝜃, are often needed in practical calculations. Next, we express these metric elements in terms of the cylindrical coordinates (R,Z) and their partial derivatives with respect to ψ and 𝜃. Note that, in this case, the coordinate system is (ψ,𝜃,ϕ) while R and Z are functions of ψ and 𝜃, i.e.,
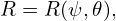 | (201) |
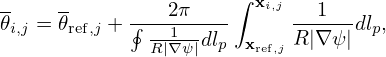 | (202) |
Then ∇R and ∇Z are written as
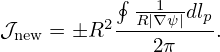 | (203) |
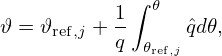 | (204) |
wehre Rψ ≡ ∂R∕∂ψ, etc. Equations (203) and (204) can be solved to give
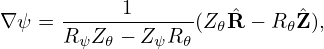 | (205) |
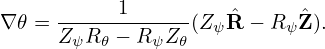 | (206) |
Using the above expressions, the Jacobian of (ψ,𝜃,ϕ) coordinates, 𝒥 , is written as
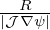
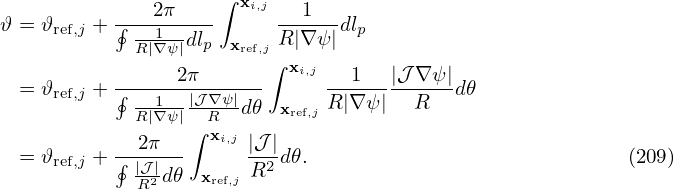 | (208) |
Using this, Expressions (205) and (206) are written as
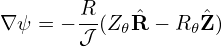 | (209) |
and
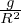 | (210) |
Then the elements of the metric matrix are written as
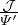 | (211) |
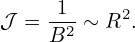 | (212) |
and
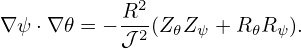 | (213) |
Equations (211), (212), and (213) are the expressions of the metric elements in terms of R, Rψ, R𝜃, Zψ, and Z𝜃. [Combining the above results, we obtain
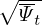 | (214) |
Equation (213) is used in GTAW code. Using the above results, hαβ = 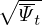 ∇α ⋅∇β are written
as
∇α ⋅∇β are written
as
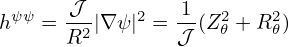 | (215) |
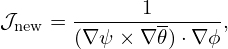 | (216) |
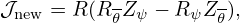 | (217) |
As a side product of the above results, we can calculate the arc length in the poloidal plane along a constant ψ surface, dℓp, which is expressed as