Deﬁnition of the ﬁeld-line-following coordinates (ψ,𝜃,α)

13.1 Deﬁnition of the ﬁeld-line-following coordinates (ψ,𝜃,α)

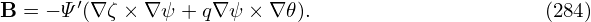
In (ψ,𝜃,ζ) coordinates, a magnetic ﬁeld line is straight in (𝜃,ζ) plane with slope being q. Then the equation for a magnetic ﬁeld line is written as

ζ = q𝜃 + α,

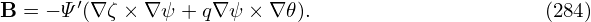(292)

where α is a constant in (𝜃,ζ) plane and can be used to label magnetic ﬁeld lines on a magnetic surface. This motivates us to use α, i.e.,

α ≡ ζ − q𝜃,

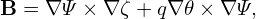(293)

to replace ζ. Then the magnetic ﬁeld in Eq. (262) is written as

B = Ψ ′∇ ψ × ∇α,

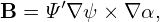(294)

which is called the Clebsch form. The direction

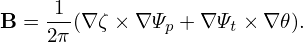∂r --|ψ,α = 𝒥∇ α× ∇ ψ, ∂𝜃

(295)

is parallel (or anti-parallel) to the magnetic ﬁeld direction. Due to this fact, (ψ,𝜃,α) coordinates are usually called “ﬁeld-line-following coordinates” or “ﬁeld-aligned coordinates” [2, 6].

Equation (294) implies that

B ⋅∇α = 0,

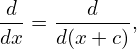(296)

and

B ⋅∇ψ = 0,

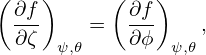(297)

i.e., both α and ψ are constant along a magnetic ﬁeld line. Taking scalar product of Eq. (294) with ∇𝜃, we obtain

′ B ⋅∇ 𝜃 = − Ψ-, 𝒥

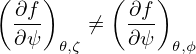(298)

which is nonzero, i.e., only 𝜃 among (ψ,𝜃,α) is changing along a magnetic ﬁeld line. (Here 𝒥 = (∇ψ ×∇𝜃 ⋅∇α)⁻¹ is the Jacobian of the coordinate system (ψ,𝜃,α), which happens to be equal to the Jacobian of (ψ,𝜃,ζ) coordinates.)

Using Eq. (294), the magnetic diﬀerential operator B ⋅∇ in the new coordinate system (ψ,𝜃,α) is written

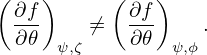Ψ ′∂ B ⋅∇f = −-𝒥 ∂𝜃f,

(299)

which is just a partial derivative over 𝜃, as is expected, since only 𝜃 is changing along a magnetic ﬁeld line.

By the way, note that (B ⋅∇α)∕(B ⋅∇𝜃) = 0, i.e., the magnetic ﬁeld lines are straight with zero slope on (𝜃,α) plane.

Using Eqs. (293) and (256), α can be written as

∫ 𝜃 α = ϕ − ˆqd𝜃, (300) 0

where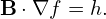

= B ⋅∇ϕ∕B ⋅∇𝜃 is the local safety factor. (If we choose the straight-ﬁeld-line 𝜃, then α is written as α = ϕ−q𝜃.) Deﬁne δ = ∫ ₀^𝜃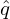

d𝜃, which is called tor_shift in TEK code, then α = ϕ−δ. In TEK, I choose 𝜃 ∈ [−π,π) with 𝜃 = −π corresponding to the high-ﬁeld-side midplane, and 𝜃 is increasing along the counter-clockwise direction viewed along ∇ϕ. The 𝜃 cut, i.e., 𝜃 = ±π is far away from the low-ﬁeld-side where ballooning modes often have larger amplitude. The (x,y) grid near the 𝜃 cut is highly twisted in real space and interplation is needed in mapping physical quantity from the grid at 𝜃 = −π plane to that at 𝜃 = +π. Numerical errors more likely appear there. So we prefer that the 𝜃 cut is located in less important area (area where mode amplitude is small).

It is widely believed that turbulence responsible for energy transport in tokamak plasmas usually has k_∥≪ k_⊥, where k_∥ and k_⊥ are the parallel and perpendicular wavenumbers, respectively. Due to this elongated structure along the parallel direction, less grids can be used in the parallel direction than that in the perpendicular direction in turbulence simulation. In this case, the ﬁeld-aligned coordinates (ψ,𝜃,α) provide suitable coordinates to be used, where less gridpoints can be used for 𝜃 coordinate in simulations and even some ∂∕∂𝜃 derivatives can be neglected (high-n approximation), which simpliﬁes the equations that need to be solved. There is another reason why almost all gyrokinetic codes use ﬁeld-aligned coordinates: the stability of numerical algorthims is improved when we use coarse grids in the parallel direction because the parallel Courant condition (for explicit schemes) Δt ≤ ΔL_∥∕v_∥ can be more easily satisﬁed (especially for the cases with kinetic electrons), where ΔL_∥ is the parallel grid spacing, which is larger when coarse grids are used in the parallel direction. This is also mentioned in Ref. [21] and it seems to be right from my experiences of testing several algorithm but a strict test is needed to verify this. This can also be understood in the following way: the coarse parallel grid automatically ﬁlters out physically irrelevant but numerically problematic high-k_∥ modes, permitting much longer time steps for explicit time stepping, in both particle and ﬂuid codes[12].

[next] [front] [up]