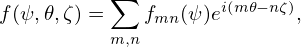
The fact B ⋅∇α = 0 implies that α is constant along a magnetic field line. At first glance, a magnetic line on an irrational surface seems to sample all the points on the surface. This seems to indicate that α is a flux surface label for irrational surface. However, α must be a non-flux-surface-function so that it can provide a suitable toroidal coordinate. I had once been confused by this conflict for a long time. The key point to resolve this confusion is to realize that it is wrong to say there is only one magnetic line on an irrational surface, i.e. it is wrong to say a magnetic line on an irrational surface samples all the points on the surface. There are still infinite number of magnetic field lines that can not be connected with each other on an irrational surface. Then the fact B ⋅∇α = 0 does not imply that α must be the same on these different magnetic field lines. In fact, although B ⋅∇α = 0, the gradient of α on a flux-surface along the perpendicular (to B) direction is nonzero, i.e., B ×∇Ψ ⋅∇α≠0. [Proof:
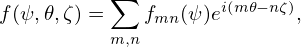
In (ψ,𝜃,ϕ) coordinates, ∇ϕ is perpendicular to ∇ψ. However, in field-line-following coordinates (ψ,𝜃,α), ∇α is not perpendicular to ∇ψ. Therefore ∇α is not along the binormal direction B ×∇ψ.