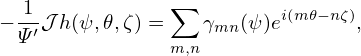Expression of ∇α, ∇ψ ⋅∇α, and ∇α ⋅∇𝜃

13.3 Expression of ∇α, ∇ψ ⋅∇α, and ∇α ⋅∇𝜃

The generalized toroidal angle α is deﬁned by Eq. (300), i.e., α = ϕ −δ, where δ = ∫ ₀^𝜃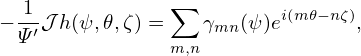 d𝜃. The gradient of α is then written as

∇ α = ∇ ϕ− ∇ δ ˆ - - = ϕ-− ∂δ∇ ψ − ∂δ∇ 𝜃. (302) R ∂ψ ∂𝜃

Then

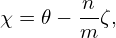∂δ 2 ∂δ ∇ ψ ⋅∇α = − ∂ψ|∇ψ | − ∂𝜃∇ ψ⋅∇ 𝜃

(303)

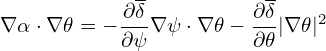- - ∂δ- ∂δ- 2 ∇α ⋅∇ 𝜃 = − ∂ψ∇ ψ ⋅∇𝜃 − ∂𝜃|∇𝜃|

(304)

Another method of computing the above quantities: Using Eqs. (209) and (210), expression (302) is written as

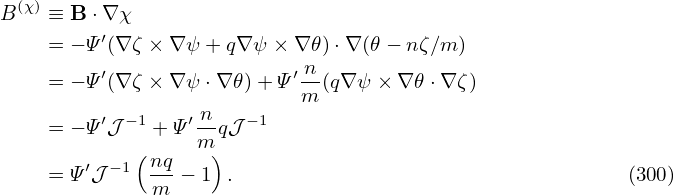
- - ˆϕ ∂δ R ∂ δR ∇ α = R-+ ∂ψ-𝒥-(Z 𝜃ˆR − R𝜃ˆZ)− ∂-𝜃𝒥-(ZψˆR − Rψ ˆZ) ˆ ( - - ) ( - - ) = ϕ-+ -∂δR-Z𝜃 − ∂δR-Zψ Rˆ+ ∂δ-RR ψ −-∂δR-R 𝜃 ˆZ. (305) R ∂ψ 𝒥 ∂𝜃𝒥 ∂𝜃𝒥 ∂ ψ𝒥

(Note that ∂δ∕∂ψ is discontinuous across the 𝜃 cut.) Then

( ) [ ˆ ( - - ) ( - - ) ] ∇ψ ⋅∇ α = − RZ 𝜃ˆR + R-R𝜃ˆZ ⋅ ϕ- + ∂δ-R-Z𝜃 − ∂δR-Zψ ˆR + ∂δR-R ψ − ∂-δR-R𝜃 ˆZ 𝒥 𝒥 R ∂ψ 𝒥 ∂𝜃𝒥 ∂𝜃𝒥 ∂ψ 𝒥 R ( ∂δ R ∂δR ) R ( ∂δR ∂δ R ) = − --Z𝜃 -----Z𝜃 − ----Zψ + --R 𝜃 ----Rψ − -----R𝜃 . (306) 𝒥 ∂ψ 𝒥 ∂𝜃𝒥 𝒥 ∂𝜃𝒥 ∂ψ 𝒥

[ ˆ ( - - ) ( - - ) ] ( ) ∇α ⋅∇ 𝜃 = ϕ- + ∂δ-R-Z𝜃 − ∂δR-Zψ ˆR + ∂δR-R ψ − ∂-δR-R𝜃 ˆZ. ⋅ R-ZψRˆ− RR ψˆZ R ∂ψ 𝒥 ∂𝜃𝒥 ∂𝜃𝒥 ∂ψ 𝒥 𝒥 𝒥 ( ∂δ R ∂δ R ) R (∂δ R ∂δ R ) R = ∂ψ-𝒥 Z 𝜃 − ∂𝜃-𝒥-Zψ 𝒥-Zψ − ∂𝜃-𝒥-Rψ − ∂ψ-𝒥-R𝜃 𝒥-Rψ. (307)

The ﬁgures below plot the spatial variation of some quantities.

pict pict

Fig. 14: The value of 𝜃, α and their gradients on an annulus on the poloidal plane (R,Z). Note that ∇𝜃 is single-valued while ∂α∕∂R and ∇α are multi-valued and thus there is a jump near the branch cut when a single branch is chosen.

pict

pict pict

Fig. 15: The same as Fig. 14, but gradients are computed in cylindrical coordinates. The results agrees with those of Fig. 14, which provides the conﬁdence in the correctness of the numerical implementation.

[next] [prev] [prev-tail] [front] [up]