13.4 Field-aligned coordinates in GEM[7] and GENE[13] codes

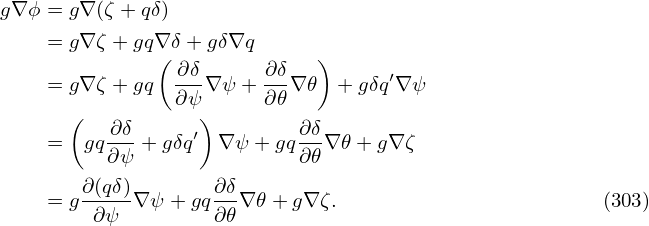
In GEM[7] and GENE[13] codes, the field-aligned coordinates (x,y,z) are defined by

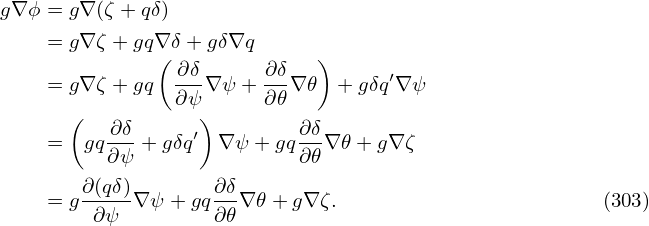(308)

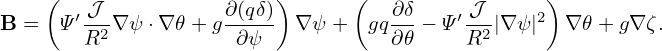(309)

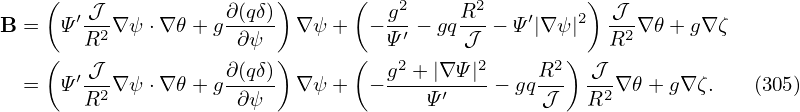(310)

where r is an arbitrary flux surface label with length dimension, which is often chosen in GEM to be the minor radius of a magnetic surface in the midplane. Here r₀ and R₀ are constant quantities of length dimension, r₀ is the minor radius of a reference magnetic surface (usually corresponding to the center of the radial simulation box), R₀ is the major radius of the magnetic axis, q₀ is the safety factor value on the r = r₀ surface. The constant length q₀R₀ introduced in the definition of z is to make z approximately correspond to the length along the field line in the large-aspect ratio limit. The constant length r₀∕q₀ introduced in the definition of y is to make y corresponds to the arc-length in the poloidal plane traced by a field line when its usual toroidal angle increment Δϕ is α. This explanation makes y look like a poloidal coordinate whereas y is actually a toroidal coordinate.

Next, let us calculate the wave number along the y direction, k_y, for a mode with toroidal wave number n. The wavelength along the y direction, λ_y, is given by

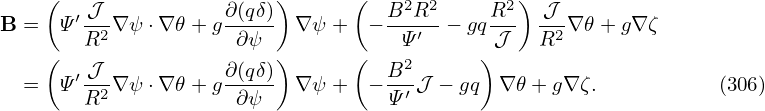(311)

Then the wavenumber k_y is written as

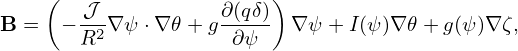(312)

On the other hand, the poloidal wavenumber k_𝜃 is given by

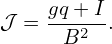(313)

where m is the poloidal mode number of the mode in (ψ,𝜃,ϕ) coordinates. If the mode has the property k_∥≈ 0, i.e., m ≈ nq₀, then k_𝜃 is equal to the k_y. The motivation of introducing the constant length r₀∕q₀ in the definition of y is to make k_y ≈ k_𝜃 for a mode with k_∥≈ 0.

Some authors call k_y or k_𝜃 by the name “binormal wavenumber”, which is not an appropriate name in my opinion. Some authors call y the binormal direction, which is also an inappropriate name since neither ∇y nor ∂r∕∂y is along the binormal direction B₀ ×∇ψ.