[next] [prev] [prev-tail] [tail] [up]

15.2 Finite difference form of toroidal elliptic operator in general coordinate system

The toroidal elliptic operator in Eq. (392) can be written

2 △ ∗Ψ = R--[(hψψΨψ)ψ + (h 𝜃𝜃Ψ𝜃)𝜃 + (hψ𝜃Ψ𝜃)ψ + (hψ𝜃Ψψ)𝜃], 𝒥
(396)

where haβ is defined by Eq. (151), i.e.,

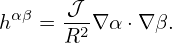𝒥 hαβ = -2∇ α⋅∇ β. R
(397)

Next, we derive the finite difference form of the toroidal elliptic operator. The finite difference form of the term (hψψΨψ)ψ is written

[ ( ) ( ) ] (hψψΨ ) | = -1- hψψ Ψi,j+1-−-Ψi,j- − hψψ Ψi,j −-Ψi,j−1 ψ ψ i,j δψ i,j+1∕2 δψ i,j− 1∕2 δψ = H ψψ (Ψi,j+1 − Ψi,j)− H ψψ (Ψi,j − Ψi,j−1), (398) i,j+1∕2 i,j− 1∕2
where
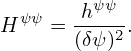ψψ -hψψ- H = (δψ)2.
(399)

The finite difference form of (h𝜃𝜃Ψ𝜃)𝜃 is written

1 [ ( Ψ − Ψ ) (Ψ − Ψ )] (h𝜃𝜃Ψ𝜃)𝜃|i,j = -- h 𝜃𝜃i+1∕2,j -i+1,j---i,j- − h𝜃i𝜃−1∕2,j -i,j----i−1,j δ𝜃 δ𝜃 δ𝜃 = Hi𝜃𝜃+1∕2,j(Ψi+1,j − Ψi,j)− H𝜃i𝜃−1∕2,j(Ψi,j − Ψi−1,j), (400)
where
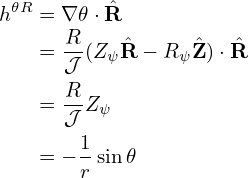𝜃𝜃 -h𝜃𝜃- H = (δ𝜃)2.
(401)

The finite difference form of (hψ𝜃Ψ𝜃)ψ is written as

[ ( ) ( )] (Ψ hψ𝜃) || = -1- hψ𝜃 Ψi+1,j+1∕2 −-Ψi−1,j+1∕2 − hψ𝜃 Ψi+1,j−-1∕2 −-Ψi−1,j−1∕2 . 𝜃 ψ i,j δψ i,j+1∕2 2δ𝜃 i,j−1∕2 2δ𝜃
(402)

Approximating the value of Ψ at the grid centers by the average of the value of Ψ at the neighbor grid points, Eq. (402) is written as

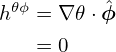(Ψ𝜃hψ𝜃)ψ|i,j = H ψi,𝜃j+1∕2(Ψi+1,j+Ψi+1,j+1− Ψi−1,j− Ψi−1,j+1)− H ψi,𝜃j−1∕2(Ψi+1,j− 1+ Ψi+1,j− Ψi−1,j−1− Ψi− 1,j).
(403)

where

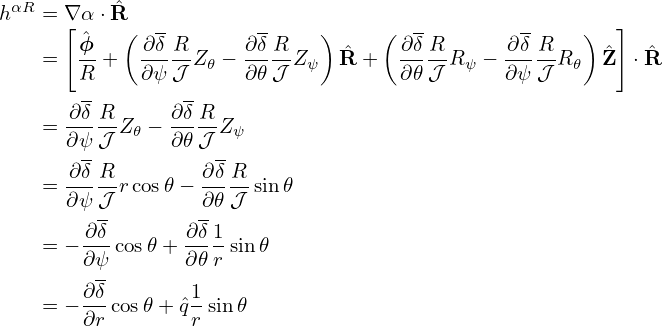ψ𝜃 -hψ𝜃-- H = 4δψd𝜃.
(404)

Similarly, the finite difference form of (hψ𝜃Ψψ)𝜃 is written as

[ ( ) ( )] ψ𝜃 1- ψ𝜃 Ψi+1∕2,j+1 −-Ψi+1∕2,j−1 ψ𝜃 Ψi−-1∕2,j+1 −-Ψi−1∕2,j−1 (Ψψh )𝜃|i,j = δ𝜃 hi+1∕2,j 2δψ − hi−1∕2,j 2δψ ψ𝜃 ψ𝜃 = H i+1∕2,j(Ψi+1,j+1 + Ψi,j+1 − Ψi+1,j−1 − Ψi,j−1) − H i−1∕2,j(Ψi,j+1 + Ψi−1,j+1 − Ψi,j−1 − Ψi− 1,(j−4015).)
Using the above results, the finite difference form of the operator 𝒥△⋆Ψ∕R2 is written as
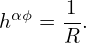
| -𝒥-△∗Ψ || = (h ψ𝜃Ψ ) + (h ψψΨ ) + (h𝜃𝜃Ψ ) + (h ψ𝜃Ψ ) R2 |i,j 𝜃ψ ψ ψ 𝜃 𝜃 ψ 𝜃 = Hψψ (Ψ − Ψ ) − Hψψ (Ψ − Ψ ) i,j+1∕2 i,j+1 i,j i,j−1∕2 i,j i,j−1 + H𝜃i𝜃+1∕2,j(Ψi+1,j − Ψi,j) − H𝜃i𝜃−1∕2,j(Ψi,j − Ψi−1,j) + Hψ𝜃 (Ψ + Ψ − Ψ − Ψ )− H ψ𝜃 (Ψ + Ψ − Ψ − Ψ ) i,j+1∕2 i+1,j i+1,j+1 i− 1,j i−1,j+1 i,j−1∕2 i+1,j−1 i+1,j i− 1,j−1 i−1,j + Hψi𝜃+1∕2,j(Ψi+1,j+1 +Ψi,j+1 − Ψi+1,j− 1 − Ψi,j−1)− Hiψ−𝜃1∕2,j(Ψi,j+1 + Ψi− 1,j+1 − Ψi− 1,j−1 − Ψi,j−1) ψψ ψψ 𝜃𝜃 𝜃𝜃 = Ψi,j(− Hi,j+1∕2 − H i,j− 1∕2 − H i+1∕2,j − H i−1∕2,j) + Ψi− 1,j−1(H ψi,𝜃j−1∕2 +H ψi𝜃−1∕2,j) +Ψi,j−1(H ψi,ψj− 1∕2 − H ψi+𝜃1∕2,j +H ψi𝜃−1∕2,j) ψ𝜃 ψ𝜃 𝜃𝜃 ψ 𝜃 ψ𝜃 + Ψi+1,j− 1(− Hi,j−1∕2 − H i+1∕2,j)+ Ψi−1,j(Hi−1∕2,j − Hi,j+1∕2 + Hi,j−1∕2) + Ψi+1,j(H 𝜃𝜃 + Hψ𝜃 − Hψ𝜃 )+ Ψi− 1,j+1(− Hψ𝜃 − H ψ𝜃 ) i+1∕2,j i,j+1∕2 i,j−1∕2 i,j+1∕2 i−1∕2,j + Ψi,j+1(H ψi,ψj+1∕2 + Hψi𝜃+1∕2,j − Hψi𝜃−1∕2,j)+ Ψi+1,j+1(H ψi,𝜃j+1∕2 + H ψi+𝜃1∕2,j)
The coefficients are given by
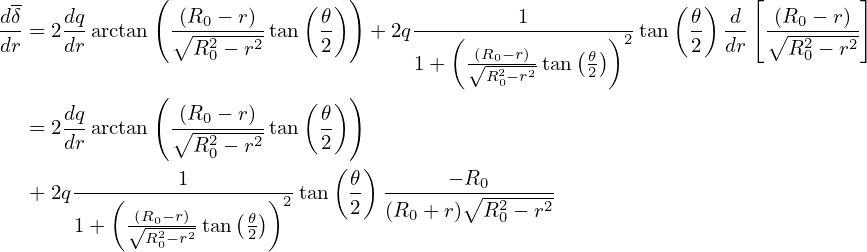ψψ 𝒥 2 1 2 2 h = R2-|∇ ψ| = 𝒥-(R𝜃 + Z𝜃),
(406)

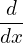𝒥 1 h𝜃𝜃 = -2|∇ 𝜃|2 = -(R2ψ + Z2ψ ), R 𝒥
(407)

and

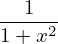hψ𝜃 = 𝒥-∇ ψ ⋅∇𝜃 = −-1(R R + Z Z ), R2 𝒥 𝜃 ψ 𝜃 ψ
(408)

where the Jacobian

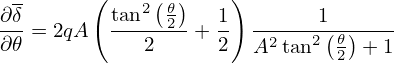𝒥 = R (R 𝜃Zψ − R ψZ𝜃).
(409)

The partial derivatives, R𝜃, Rψ, Z𝜃, and Zψ, appearing in Eqs. (406)-(409) are calculated by using the central difference scheme. The values of hψψ, h𝜃𝜃, hψ𝜃 and 𝒥 at the middle points are approximated by the linear average of their values at the neighbor grid points.

[next] [prev] [prev-tail] [front] [up]