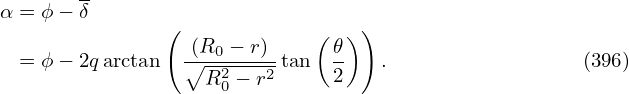
Next we derive the form of the GS equation in a general coordinate system. The main task is to derive the form of the toroidal elliptic operator in the general coordinate system. The toroidal elliptic operator takes the form
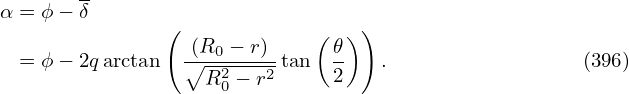 | (391) |
For an arbitrary general coordinate system (ψ,𝜃,ϕ) (the (ψ,𝜃,ϕ) coordinate system here is an arbitrary general coordinate system except that ∇ϕ is perpendicular to both ∇ψ and ∇𝜃), the toroidal elliptic operator is written
![2 {[ ] [ ] [ ] [ ] }
△ ⋆Ψ = R-- Ψ ψ 𝒥-|∇ ψ|2 + Ψ𝜃 𝒥-|∇ 𝜃|2 + Ψψ 𝒥-(∇ ψ⋅∇ 𝜃) + Ψ𝜃 𝒥-∇𝜃 ⋅∇ψ ,
𝒥 R2 ψ R2 𝜃 R2 𝜃 R2 ψ](tokamak_equilibrium518x.png) | (392) |
where the subscripts denotes partial derivatives, 𝒥 is the Jacobian of the coordinate system (ψ,𝜃,ϕ). [Next, we provide the proof of Eq. (392). The gradient of Ψ is written as (note that Ψ is independent of ϕ)
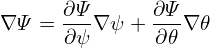 | (393) |
Using this expression and the divergence formula (110), the elliptic operator in Eq. (391) is written
![( 1 ∂Ψ 1 ∂Ψ )
△ ∗Ψ = R2 ∇ ⋅ R2-∂ψ-∇ψ + R2-∂𝜃-∇𝜃
( )
= R2 1--∂- 𝒥 -1-∂Ψ-∇ψ ⋅∇ ψ+ 𝒥 -1-∂Ψ-∇𝜃 ⋅∇ ψ
𝒥 ∂ψ ( R2 ∂ψ R2 ∂𝜃 )
2 1-∂- -1-∂Ψ- -1-∂Ψ-
+ R 𝒥 ∂𝜃 𝒥 R2 ∂ψ∇ ψ ⋅∇𝜃 +𝒥 R2 ∂𝜃 ∇𝜃 ⋅∇𝜃
2[ ( ) ( ) ( ) ( ) ]
= R-- Ψψ-𝒥2|∇ψ|2 + Ψ𝜃-𝒥2∇ ψ⋅∇ 𝜃 + Ψψ 𝒥2∇ ψ⋅∇ 𝜃 + Ψ𝜃-𝒥2|∇ 𝜃|2 (39,4)
𝒥 R ψ R ψ R 𝜃 R 𝜃](tokamak_equilibrium520x.png)
Using Eq. (392), the GS equation (66) is written
![[( ) ( ) ( ) ( ) ]
R2- Ψ 𝒥-|∇ ψ|2 + Ψ 𝒥-|∇𝜃|2 + Ψ 𝒥--∇ψ ⋅∇𝜃 + Ψ -𝒥-∇ψ ⋅∇ 𝜃 = − μ R2 dP− dg-g,
𝒥 ψR2 ψ 𝜃R2 𝜃 𝜃R2 ψ ψR2 𝜃 0 dΨ dΨ](tokamak_equilibrium521x.png) | (395) |
which is the form of the GS equation in (ψ,𝜃,ϕ) coordinate system.