[next] [prev] [prev-tail] [tail] [up]

15.6 Fixed boundary equilibrium numerical code

The tokamak equilibrium problem where the shape of the LCFS is given is called fixed boundary equilibrium problem. I wrote a numerical code that uses the iterative metric method[11] to solve this kind of equilibrium problem. Figure 30 describes the steps involved in the iterative metric method.

pict pict

pict pict

pict

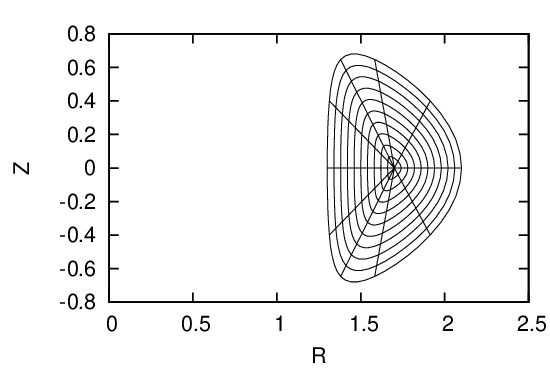
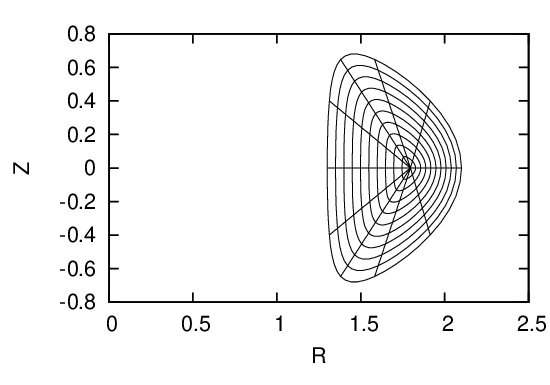
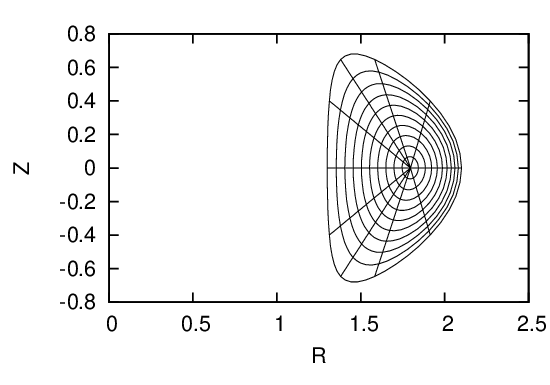
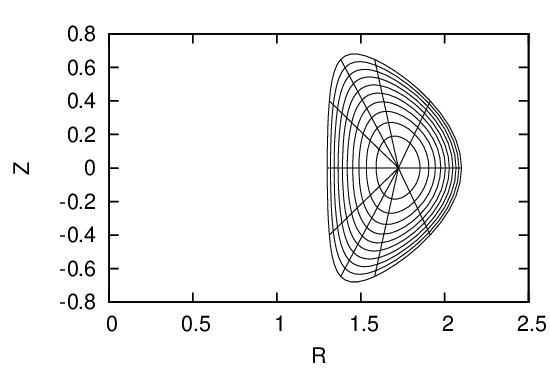
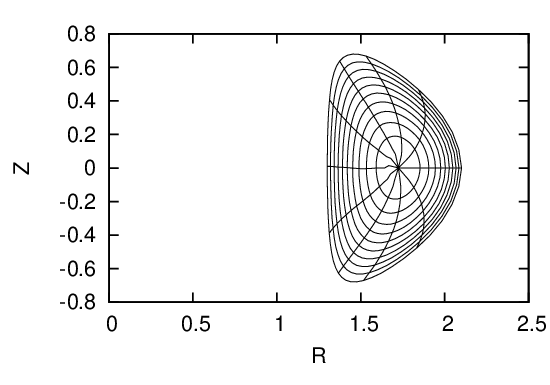
Fig. 30: Upper left figure plots the initial coordinate surfaces. After solving the GS equation to obtain the location of the magnetic axis, I shift the origin point of the initial coordinate system to the location of the magnetic axis (upper right figure). Then, reshape the coordinate surface so that the coordinate surfaces ψ = const lies on magnetic surfaces (middle left figure). Recalculate the radial coordinate ψ that is consistent with the Jacobian constraint and interpolate flux surface to uniform ψ coordinates (middle right figure). Recalculate the poloidal coordinate 𝜃 that is consistent with the Jacobian constraint and interpolate poloidal points on every flux surface to uniform 𝜃 coordinates (bottom left figure).

[next] [prev] [prev-tail] [front] [up]