A

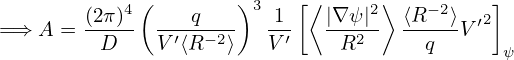
[In passing, we note that Ψ ≡ A_ϕR is the covariant toroidal component of A in cylindrical coordinates (R,ϕ,Z). The proof is as follows. Note that the covariant form of A should be expressed in terms of the contravariant basis vector (∇R, ∇ϕ, and ∇Z), i.e.,

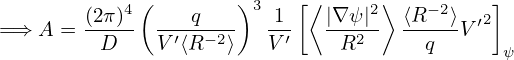(505)

where A₂ is the covariant toroidal component of A. To obtain A₂, we take scalar product of Eq. (505) with ∂r∕∂ϕ and use the orthogonality relation (80), which gives

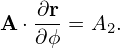(506)

In cylindrical coordinates (R,ϕ,Z), the location vector is written as

(507)

where 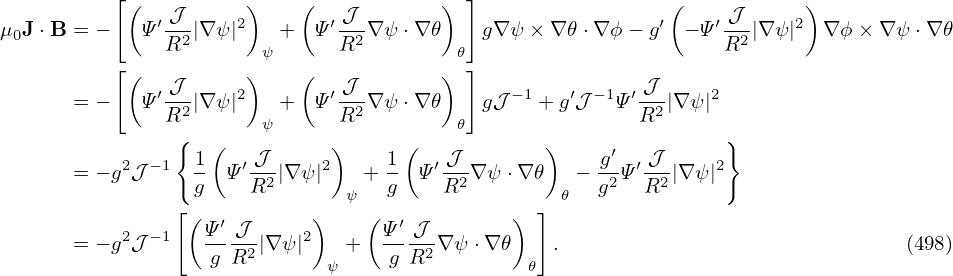, , 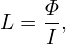and 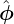are unit vectors along ∂r∕∂R, ∂r∕∂Z, and ∂r∕∂ϕ, respectively, i.e.

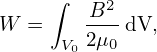(508)

Using this, we obtain

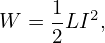(509)

Use Eq. (509) in Eq. (506) giving

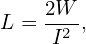(510)

with A_ϕ defined by A_ϕ = A ⋅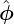. Equation (510) indicates that Ψ = A_ϕR is the covariant toroidal component of the vector potential.]