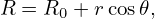
Define (r,𝜃,ϕ) coordinates by
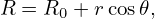 | (574) |
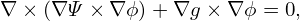 | (575) |
where (R,ϕ,Z) are the cylindrical coordinates and R0 is a constant. The above transformation is shown graphically in Fig. 40.
The Jacobian of (r,𝜃,ϕ) coordinates can be calculated using the definition. Using x = R cosϕ, y = R sinϕ, and z = Z, the Jacobian (with respect to the Cartesian coordinates (x,y,z)) is written as
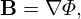
Next, we transform the GS equation from (R,Z) coordinates to (r,𝜃) coordinates. Using the relations R = R0 + r cos𝜃 and Z = r sin𝜃, we have
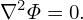 | (577) |
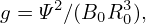 | (578) |
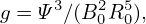 | (579) |
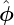 | (580) |
The GS equation in (R,Z) coordinates is given by
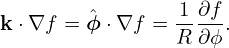 | (581) |
The term ∂Ψ∕∂Z is written as
Using Eq. (582), ∂2Ψ∕∂Z2 is written as
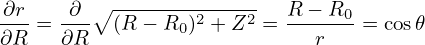 | (584) |
sin𝜃 = 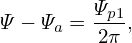 . .
|
cos𝜃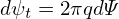 = −Z = −Z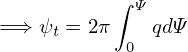
|
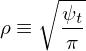 | (585) |
cos𝜃 = 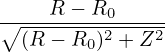
|
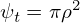 | (586) |
Summing the the right-hand-side of Eq. (583) and the expression on line (587) yields
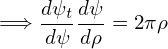 | (589) |
Using these, the GS equation is written as
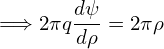 + +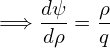  + + 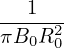 − −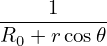  = −μ0(R0+r cos𝜃)2 = −μ0(R0+r cos𝜃)2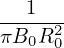 − −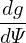 g(Ψ), g(Ψ),
|
which can be arranged in the form
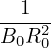 | (590) |
which agrees with Eq. (3.6.2) in Wessson’s book[27], where f is defined by f = RBϕ∕μ0, which is different from g ≡ RBϕ by a 1∕μ0 factor.