[prev] [prev-tail] [tail] [up]

C.4 Computing Fourier integrals using FFT (not finished, to be deleted)

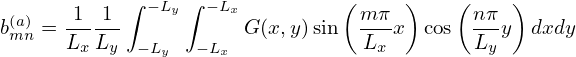
Consider the calculation of the following integral:

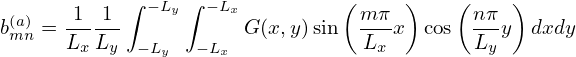∫ b I(ω ) = eiωth(t)dt. a
(138)

Divide the interval [a,b] into M uniform sub-intervals and define

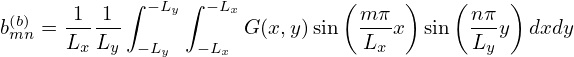b− a Δ = ----,tj = a + Δj,hj = h(tj),j = 0,1,2,...,M M
(139)

Then the integration in Eq. (138) can be approximated as

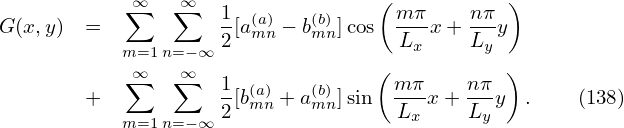M−1 I(ω) ≈ Δ ∑ hj exp (iωtj). j=0
(140)

Define ωm = 2πm∕(MΔ) with integer m and −M∕2 < m < M∕2. Consider the calculation of I(ωm). Using Eq. (140), we obtain

M∑ −1 I(ωm) = Δ hjexp[iωm (a+ Δj)] j=0 iω a M∑−1 = Δe m hjexp(iωm Δj) j=0 iω a M∑−1 ( 2πm ) = Δe m hjexp i-M--j j=0 = ΔeiωmaHm (141) = Δeiωma[DFT (h0,h1,h2,...,hM −1)]m. (142)
Equation (142) indicates the value of the integration I(ωm) can be obtained by calculating the discrete Fourier transformation of hj. However, as discussed in Ref. [2], equation (142) is not recommended for practical use because the oscillatory nature of the integral will make Eq. (142) become systematically inaccurate as ω increases. Next, consider a new method, in which h(t) is expanded as
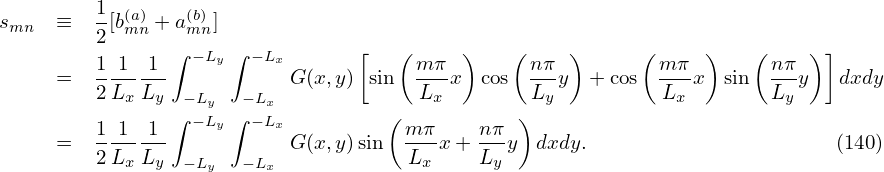M ( ) ( ) h(t) ≈ ∑ hjψ t−-tj + ∑ hjφj t−-tj j=0 Δ j=endpoints Δ
(143)

Apply the integral operator∫ abdtexp(iωt) to both sides of Eq. (143), we obtain

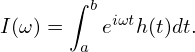∫ b iωt ∑M ∫ b ( t− tj) iωt ∑ ∫ b (t − tj) iωt h(t)e dt ≈ hj ψ -Δ--- e dt+ hj φj --Δ-- e dt. a j=0 a j=endpoints a
(144)

Make the change of variables s = (t−tj)∕Δ in the first integral and s = (t−a)∕Δ in the second integral, the above equation is written as

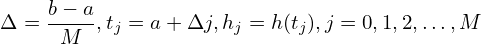∫ b ∑M ∫ b ∑ ∫ b h(t)eiωtdt ≈ Δ hj ψ(s)eiω(Δs+tj)ds+ Δ hj φj (s− j)eiω(Δs+a)ds a j=0 a j=endpoints a
(145)

Define 𝜃 = ωΔ and make use of tj = a + jΔ, the above equation is written as

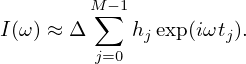∫ b iωt iωa M∑ i𝜃j∫ b i𝜃s iωa ∑ ∫ b i𝜃s a h(t)e dt ≈ Δe hje a ψ(s)e ds+ Δe hj a φj(s− j)e ds j=0 j=endpoints
(146)

Define

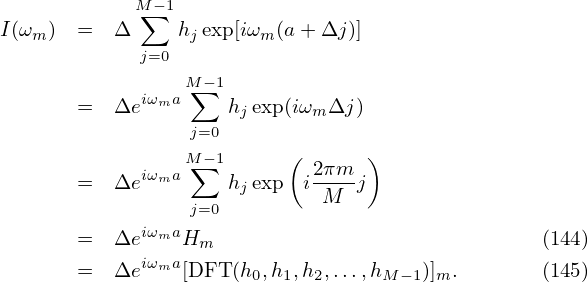∫ b W (𝜃) = ψ (s)ei𝜃sds a
(147)

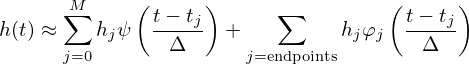∫ b αj(𝜃) = φj(s− j)ei𝜃sds a
(148)

Then Eq. (146) is written as

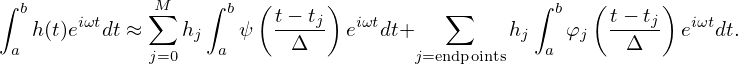⌊ ⌋ ∫ b iωt iωa⌈ ∑M i𝜃j ∑ ⌉ a h (t)e dt ≈ Δe W (𝜃) hje + hjαj(𝜃) . j=0 j=endpoints
(149)

 

 

 

 

 

pict

Figure 9: Older version of Fig. 2, created by Metapost, the new version is created by the vector graphic editor in TeXmacs.

 

[prev] [prev-tail] [front] [up]