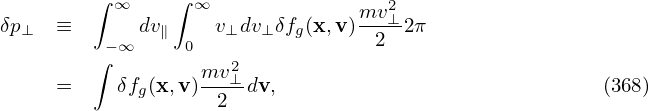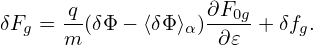
The perturbed distribution function δF given in Eq. () contains two terms. The first term is gyro-phase dependent while the second term is gyro-phase independent. The perpendicular velocity moment of the second term will give rise to the so-called diamagnetic flow. For this case, it is crucial to distinguish between the distribution function in terms of the guiding-center variables, fg(X,v), and that in terms of the particle variables, fp(x,v). In terms of these denotations, equation () is written as
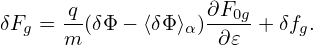 | (357) |
Next, consider the perpendicular flow U⊥ carried by δfg. This flow is defined by the corresponding distribution function in terms of the particle variables, δfp, via,
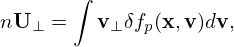 | (358) |
where n is the number density defined by n = ∫ δfpdv. Using the relation between the particle distribution function and guiding-center distribution function, equation (358) is written as
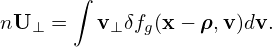 | (359) |
Using the Taylor expansion near x, δfg(x −ρ,v) can be approximated as
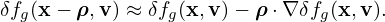 | (360) |
Plugging this expression into Eq. (359), we obtain
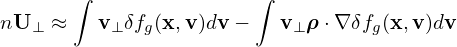 | (361) |
As mentioned above, δfg(x,v) is independent of the gyro-angle α. It is obvious that the first integration is zero and thus Eq. (361) is reduced to
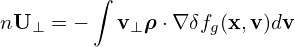 | (362) |
Using the definition ρ = −v × e∥∕Ω, the above equation is written
where H =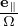 ×∇δfg(x,v), which is independent of the gyro-angle α because both e∥(x)∕Ω(x) and
δfg(x,v) are independent of α. Next, we try to perform the integration over α in Eq. (363). In terms of
velocity space cylindrical coordinates (v∥,v⊥,α), v⊥ is written as
×∇δfg(x,v), which is independent of the gyro-angle α because both e∥(x)∕Ω(x) and
δfg(x,v) are independent of α. Next, we try to perform the integration over α in Eq. (363). In terms of
velocity space cylindrical coordinates (v∥,v⊥,α), v⊥ is written as
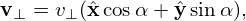 | (364) |
where 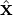 and
and 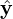 are two arbitrary unit vectors perpendicular each other and both perpendicular to
B0(x). H can be written as
are two arbitrary unit vectors perpendicular each other and both perpendicular to
B0(x). H can be written as
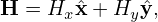 | (365) |
where Hx and Hy are independent of α. Using these in Eq. (363), we obtain
![∫
nU ⊥ = v⊥ (xˆcosα+ ˆy sinα )v⊥ (Hx cosα + Hy sinα)dv
∫
= v2⊥ [ˆx(Hx cos2α+ Hy sin αcosα) +yˆ(Hx cosα sinα + Hy sin2α)]dv. (366)](nonlinear_gyrokinetic_equation428x.png)