[next] [prev] [prev-tail] [tail] [up]

H Transform gyrokinetic equation from (X,μ,𝜀,α) to (X,μ,v∥,α) coordinates

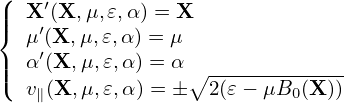
The gyrokinetic equation given above is written in terms of variables (X,μ,𝜀,α). Next, we transform it into coordinates (X′,μ′,v∥,α′) which are defined by

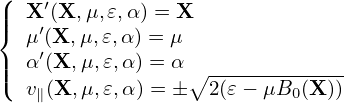( ′ ||{ X′(X,μ,𝜀,α) = X μ′(X, μ,𝜀,α) = μ ||( α (X, μ,𝜀,α) = α ∘------------- v∥(X, μ,𝜀,α) = ± 2(𝜀 − μB0 (X))
(369)

Use this definition and the chain rule, we obtain

|| ′ ′ ∂v ′ ∂--|| = ∂X--⋅ -∂′-+ ∂μ--∂′ + --∥-∂-+ ∂α--∂′ ∂X μ,𝜀,α ∂X ∂X ∂X ∂μ ∂X ∂v∥ ∂X ∂α --∂- μ-∂B0--∂- = ∂X ′ − v∥ ∂X ∂v∥, (370)
and
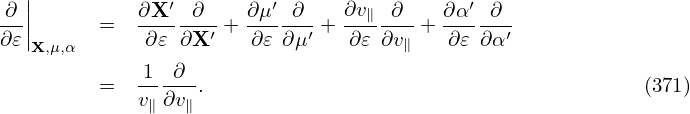
∂ || ∂X ′ ∂ ∂μ′ ∂ ∂v∥ ∂ ∂α′ ∂ ∂-𝜀|| = -∂𝜀-∂X-′ + ∂𝜀-∂μ′ + ∂𝜀-∂v + ∂𝜀-∂α′ X,μ,α ∥ = 1--∂-. (371) v∥∂v∥
Then, in terms of (X′,μ′,v∥,α′), equation (136) is written
[ ] ∂-+ (v∥e∥ + VD +δVD ) ⋅-∂-- δG0 − (v∥e∥ + VD + δVD )⋅ μ-∂B0-∂δG0- ∂t ( ∂X′) v∥∂X ∂v∥ ∂F0- -μ ∂B0∂F0- q-∂⟨δL⟩α∂F0-1- = − δVD ⋅ ∂X ′ − v∥ ∂X ∂v∥ − m ∂t ∂v∥ v∥, (372)
Dropping terms of order higher than O(λ2), equation (372) is written as
[ ] ∂- -∂-- ∂B0-∂δG0- ∂t + (v∥e∥ + VD + δVD )⋅∂X ′ δG0 − e∥ ⋅μ ∂X ∂v∥ ( ∂F ) ( ∂B q∂ ⟨δL ⟩ ) ∂F 1 = − δVD ⋅ --0′ + δVD ⋅μ---0− -------α --0--, (373) ∂X ∂X m ∂t ∂v∥v∥
The above equation drops all terms higher than O(λ2) and as a result the coefficient before ∂δf∕∂v∥ contains only the mirror force, i.e., −e∥⋅ μ∇B0, which is independent of any perturbations.

Note that the gyro-averaging operator in (X′,μ′,v∥,α′) coordinates is identical to that in the old coordinates since the perpendicular velocity variable μ is identical between the two coordinate systems. Also note that the perturbed guiding-center velocity δVD is given by

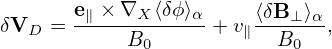e∥-×∇X-⟨δϕ⟩α ⟨δB-⊥⟩α- δVD = B0 + v∥ B0 ,
(374)

where ∂∕∂X (rather than ∂∕∂X′) is used. Since δϕ(x) = δϕg(X,μ′,α′), which is independent of v∥, then Eq. (370) indicates that ∂δϕ∕∂X = ∂δϕ∕∂X′.

Following the same procedures, equation (141) in terms of (X′,μ′,v∥,α′) is written as

[ ] ∂-+ (v e + V +δV ) ⋅-∂-- δf − e ⋅μ∇B ∂δf- ∂t ∥ ∥ D D ∂X ′ ∥ 0 ∂v∥ (∂F0 ) ∂F0 1 = − δVD ⋅ ∂X-′ +δVD ⋅μ∇B0 ∂v--v- [ ( ∥ ∥ ) ] −-q − ∂⟨v-⋅δA⟩α − v∥e∥ + VD + v∥ ⟨δB-⊥⟩α- ⋅∇X ⟨δϕ⟩α ∂F0-1-. (375) m ∂t B0 ∂v∥ v∥
next, try to recover the equation in Mishchenk’s paper:
[ ] ∂-+ (v e + V + δV )⋅-∂-- δf − e ⋅μ∇B ∂δf- ∂t ∥ ∥ D D ∂X ′ ∥ 0∂v∥ ( ∂F0) ∂F0 1 = − δVD ⋅ ∂X-′ + δVD ⋅μ ∇B0 ∂v-v- [ ( ∥ ∥ ) ] − q- − ∂⟨δA∥⟩α − e∥ + VD-+ ⟨δB⊥-⟩α- ⋅∇X ⟨δϕ⟩α ∂F0. m ∂t v∥ B0 ∂v∥
δL = δΦ − v ⋅ δA,
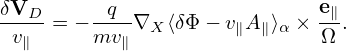δVD q e∥ -v-- = −mv--∇X ⟨δΦ − v∥A ∥⟩α × Ω-. ∥ ∥
(376)

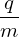−q- m[ ( ) ] − ∂⟨δA-∥⟩α-− e + VD--+ q-∇ ⟨A ⟩ × e∥ ⋅∇ ⟨δϕ⟩ ∂t ∥ v∥ m X ∥α Ω X α∂F0- ∂v∥.

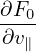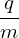−q m-[ ] ∂⟨δA ∥(h)⟩α ( VD q e∥) − ---∂t----− -v--+ m-∇X ⟨A ∥⟩α × Ω- ⋅∇X ⟨δϕ⟩α ∥∂F0 ∂v-- ∥.

 

H.1 Recover equation in W. Deng’s 2011 NF paper

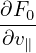The guiding-center velocity in the equilibrium field is given by

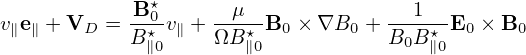B⋆ μ 1 v∥e∥ + VD = --0⋆-v∥ +---⋆-B0 × ∇B0 + ----⋆-E0 × B0 B ∥0 ΩB ∥0 B0B ∥0
(377)

where

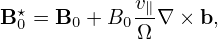⋆ v∥ B0 = B0 + B0 Ω-∇ × b,
(378)

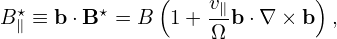( ) B ⋆∥ ≡ b ⋅B⋆ = B 1+ v∥b ⋅∇ × b , Ω
(379)

Using B∥0⋆ ≈ B0, then expression (377) is written as

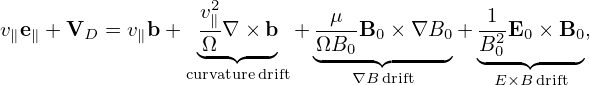2 ve + V = v b + v∥∇ × b + --μ-B × ∇B + -1-E × B , ∥ ∥ D ∥ Ω◟--◝◜--◞ ΩB0---0-----0 B20 0 0 curvaturedrift ◟ ∇B◝◜drift ◞ ◟-E×◝B◜drift◞
(380)

where the curvature drift, ∇B drift, and E0 × B0 drift can be identified. Note that the perturbed guiding-center velocity δVD is given by (refer to Sec. C.3)

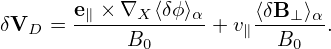e∥-×∇X-⟨δϕ⟩α ⟨δB-⊥⟩α- δVD = B0 + v∥ B0 .
(381)

Using the above results, equation (375) is written as

[ ] ∂-+ (v e + V + δV )⋅ -∂--δf − e ⋅μ∇B ∂δf- ∂t ∥ ∥ D D ∂X′ ∥ 0∂v ∥ ( ∂F0 ) ( e∥ × ∇X ⟨δϕ⟩α ⟨δB ⊥⟩α) ( μ ∂F0 ) = − δVD ⋅ ∂X-′ + -----B------+ v∥--B---- ⋅ v-∇B0 -∂v- [ ( 02 0 ∥ ∥ ) ] -q ∂⟨v-⋅δA⟩α v∥ -μ-- -1- ⟨δB-⊥⟩α ∂F0-1 −m − ∂t − v∥e∥ + Ω ∇ ×b + ΩB0 B0 × ∇B0 + B20E0 × B0 + v∥ B0 ⋅∇X ⟨δϕ⟩α ∂v(∥3v8∥2,)
Collecting coefficients before ∂F0∕∂v∥, we find that the two terms involving ∇B0 (terms in blue and red) cancel each other, yielding
[ ] ∂- -∂-- ∂δf- ∂t + (v∥e∥ + VD + δVD )⋅ ∂X′ δf − e∥ ⋅μ∇B0 ∂v ∥ ( ∂F ) = − δVD ⋅ --0- [ ∂X ( ) ] -q m- ⟨δB-⊥⟩α- ∂⟨v⋅δA-⟩α v2∥ -1- ⟨δB⊥-⟩α- ∂F0-1 +m q v∥ B0 ⋅(μ ∇B0) + ∂t + v∥b + Ω ∇ × b + B20 E0 × B0 + v∥ B0 ⋅∇X ⟨δϕ⟩α ∂v∥(v3∥8,3)
This equation agrees with Eq. (8) in I. Holod’s 2009 pop paper (gyro-averaging is wrongly omitted in that paper) and W. Deng’s 2011 NF paper.

 

 

[next] [prev] [prev-tail] [front] [up]