Polarization density matrix obtained by numerically integrating in phase space using grid

8 Polarization density matrix obtained by numerically integrating in phase space using grid

In Sec. 7, to evaluate the polarization density, the potential δΦ is Fourier expanded in space using local Cartesian coordinates, and then the double gyro-angle integration of each harmonic is expressed as the Bessel function. (It seems that the original motivation of using the Fourier expansion here is to facilitate analytical treatment and is not designed for numerical use. GEM code does make use of the local Fourier expansion in its numerical implementation, where the local perpendicular wave number needs to be estimated numerically, which seems awkward.)

In this section, we avoid using the local Fourier expansion, and directly express the double gyro-angle integral as linear combination of values of δΦ at spatial grid-points. The polarization density is given by Eq. (224), i.e.,

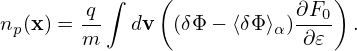∫ ( ) np(x) = q- dv (δΦ − ⟨δΦ⟩α)∂F0 . m ∂𝜀

(265)

Our goal is to write n_p in the following real-space discrete from:

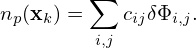∑ np(xk) = cijδΦi,j. i,j

(266)

8.1 Direct evaluation of the double gyrophase integration

Deﬁne

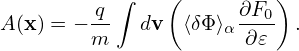q∫ ( ∂F0) A(x) = −m- dv ⟨δΦ ⟩α ∂𝜀-- .

(267)

Using dv = v_⊥dv_⊥dv_∥dα, the above integration is written as

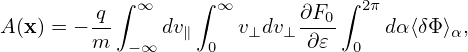q ∫ ∞ ∫ ∞ ∂F ∫ 2π A (x ) = −-- dv∥ v⊥dv⊥ --0- dα ⟨δΦ ⟩α, m −∞ 0 ∂𝜀 0

(268)

where use has been made of the assumption that ∂F₀∕∂𝜀 is uniform in α in (x,v_⊥,v_∥,α) coordinates, and thus is moved outside of the α integration. Using the deﬁnition of gyro-averaging (2π)⁻¹ ∫ ₀^2π(…)dα′, the above integration is written as

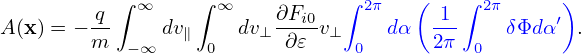∫ ∞ ∫ ∞ ∫ 2π ( ∫ 2π ) A(x) = −-q dv∥ dv⊥∂Fi0v⊥ dα 1-- δΦdα ′ . m −∞ 0 ∂𝜀 0 2π 0

(269)

Note that the gyro-averaging is performed in the guiding-center space, i.e., performed by varying the gyroangle α′ while keeping guiding-center position X, v_⊥, and v_∥ constant. Using the deﬁnition of δΦ_g (i.e., its relation with δΦ):

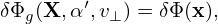δΦg(X,α′,v⊥) = δΦ(x),

(270)

where the particle location x is computed from the guiding-center location by

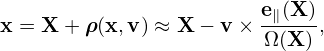e∥(X ) x = X + ρ(x,v ) ≈ X − v× Ω(X-),

(271)

then A(x) is written as

A(x) ∫ ∫ ∫ [ ∫ ( ) ] = − q- ∞ dv ∞ dv ∂Fi0v 2π dα -1- 2πδΦ X − v (v ,α ′)× e∥(X-) dα ′ m −∞ ∥ 0 ⊥ ∂𝜀 ⊥ 0 2π 0 ⊥ ⊥ Ω(X) ∫ ∞ ∫ ∞ ∫ 2π ⌊ N2 ( ) ⌋ ≈ − q- dv∥ dv⊥∂Fi0v⊥ dα⌈ 1--∑ δΦ X − v⊥(v⊥,α′)× e∥(X)- ⌉ m −∞ 0 ∂𝜀 0 N2 j=1 j Ω (X)

where v_⊥ = v(v_⊥,α_j′) denotes a perpendicular velocity corresponding to a discrete gyro-angle α_j′.

Next, in order to perform the remaining velocity space integration, transform back to the particle coordinates (because the velocity integration is performed in the particle coordinates, i.e., it is performed by keeping the particle coordinate x constant):

∫ ∫ -q ∞ ∞ ∂Fi0 A (x) = −m −∞ dv∥ 0 dv⊥ ∂𝜀 v⊥ ∫ ⌊ N ( ) ⌋ × 2π dα⌈ 1--∑2 δΦ x+ v (v ,α )× e∥(X)-− v (v ,α′)× e∥(X)- ⌉ 0 N2 j=1 ⊥ ⊥ Ω (X ) ⊥ ⊥ j Ω (X ) ∫ ∞ ∫ ∞ ≈ − q- dv∥ dv⊥ ∂Fi0-v⊥ m −∞⌊ 0 ∂ 𝜀 ⌋ ∫ 2π N∑2 ( ) × dα⌈ 1-- δΦ x+ v⊥ (v⊥,α )× e∥(x)− v⊥(v⊥,α′j)× e∥(x)- ⌉ 0 N2 j=1 Ω (x) Ω(x) q ∫ ∞ ∫ ∞ ∂F ≈ − -- dv∥ dv⊥ --i0-v⊥ m −∞ 0 ( ∂ 𝜀 ) 2π-N∑1 -1-N∑2 e∥(x) ′ e∥(x)- × N1 N2 δΦ x + v⊥(v⊥,αi)× Ω (x) − v⊥(v⊥,αj)× Ω(x) . (272) i=1 j=1

For notation ease, deﬁne

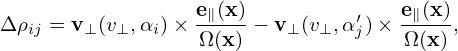e∥(x)- ′ e∥(x) Δρij = v⊥ (v⊥,αi)× Ω(x) − v⊥(v⊥,αj)× Ω (x),

(273)

where Δρ_ij is a function of (x,v_⊥,α_i,α_j′). Then Eq. (272) is written as

q ∫ ∞ ∫ ∞ ∂Fi0 2π N∑1 1 N∑2 A(x) = − m- dv∥ dv⊥-∂𝜀-v⊥ N1- N2- δΦ(x + Δρij). (274) −∞ 0 i=1 j=1

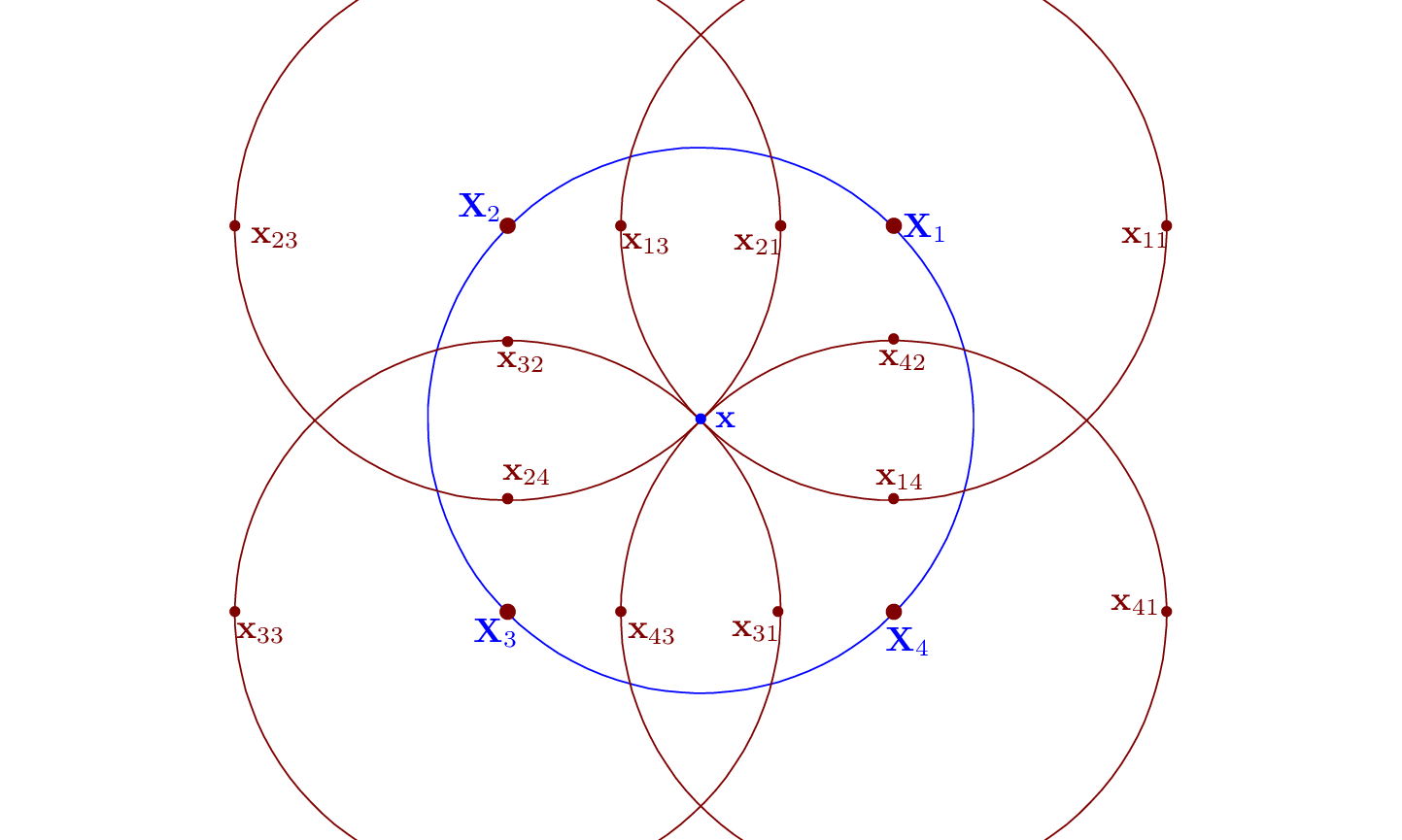
The guiding-center transform and its inverse involved in the above are illustrated in Fig. 2. Then the double gyro-angle integral appearing in the polarization density is approximated as

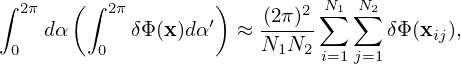∫ ( ∫ ) N1 N2 2π dα 2π δΦ (x)dα ′ ≈ -(2π)2 ∑ ∑ δΦ(x ), 0 0 N1N2 i=1 j=1 ij

(275)

where N₁ = 4,N₂ = 4 for the case shown in Fig. 2. This gives how to approximate the double gyro-angle integration using the discrete values of δΦ_ij. The spatial points x_ij appearing in Eq. (275) are not necessarily grid points. Linear interpolations are used to express δΦ(x_ij) as linear combination of values of δΦ at grid-points.

Figure 2: Given a v_⊥, then the double gyro-angle integration in Eq. (269) at a particle location x is evaluated by the following steps: Use the guiding center transform to get guiding-center locations (four locations are shown in this case, namely X_i with i = 1,2,3,4, corresponding gyro-angle α_i with i = 1,2,3,4; 2.) For each guiding-center location, use the inverse guiding-center transform to calculate points on the corresponding gyro-ring (four points are shown for each guiding-center X_i in this case, namely x_ij with j = 1,2,3,4, corresponding gyro angle α_j′ with j = 1,2,3,4.)

8.2 Performing the parallel velocity integration

Assume that F₀ is Maxwellian, then

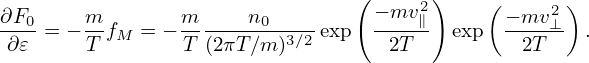( − mv2 ) ( 2) ∂F0-= − mfM = − m----n0--3∕2 exp ----∥- exp − mv-⊥ . ∂ 𝜀 T T (2πT ∕m) 2T 2T

(276)

Note that Δρ_ij is independent of v_∥. Then the integration over v_∥ in Eq. (274) can be analytically performed, yielding

∫ ∞ ( -2) ∫ ∞ ( -2 ) A(x) = q- dv∥ exp −-v∥ dv⊥v⊥--n0-- exp −v⊥- T −∞ 2 0 (2π)3∕2 2 ∑N1 ∑N2 × 2π- -1- δΦ (x + Δ ρij) N1 i=1N2 j=1 ∫ ∞ ( -2 ) N1 N2 = n0 dv⊥v⊥ exp −v⊥- -1-∑ -1-∑ q-δΦ(x+ Δ ρij). (277) 0 2 N1 i=1 N2 j=1T

where v_∥ = v_∥∕v_t, v_⊥ = v_⊥∕v_t, v_t =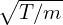 ∘T-∕m-

, and use has been made of

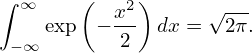∫ ∞ ( 2) √ --- exp − x- dx = 2π. −∞ 2

(278)

8.3 Toroidal DFT of polarization density in ﬁeld-aligned coordinates

In ﬁeld-aligned coordinates (x,y,z), Fourier expansion of δΦ along y is written

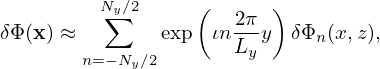Ny∑∕2 ( 2π ) δΦ (x) ≈ exp ιn L-y δΦn(x,z), n=−Ny∕2 y

(279)

where ι = √ ---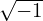
− 1 . Use this in Eq. (277), yielding

∫ ( - ) A (x) = n ∞ dv v exp −v2⊥- 0 0 ⊥ ⊥ 2 N∑1 ∑N2⌊ Ny∑∕2 ( ) ⌋ × -1- -1- ⌈ q- exp ιn 2π(y+ Δ ρijy) δΦn (x + Δρijx,z + Δρijz)⌉ N1 i=1N2 j=1 T n=−Ny∕2 Ly Nt∕2 ( ) ∫ ( - ) ∑ 2π- ∞ - - −-v2⊥ = exp ιn Lyy n0 0 dv⊥v⊥ exp 2 n=−Ny∕2 -1-N∑1 -1-∑N2[ ( 2π- ) q- ] × N1 N2 exp ιnLyΔ ρijy T δΦn(x+ Δ ρijx,z + Δ ρijz) . (280) i=1 j=1

From Eq. (280), the Fourier expansion coeﬃcient of A(x) can be identiﬁed:

∫ ∞ - - (− v2) An (x,z) = n0 dv⊥v⊥exp ---⊥ 0 [ ( 2 ) ] 1--N∑1 -1-N∑2 2π- q- × N1 N2 exp ιn LyΔ ρijy TδΦn (x + Δρijx,z + Δρijz) . (281) i=1 j=1

Let us make the following approximation

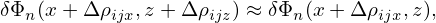δΦn(x+ Δ ρijx,z + Δ ρijz) ≈ δΦn(x + Δρijx,z),

(282)

which should be a good approximation since the variation of δΦ along a ﬁeld line over a distance of a Larmor radius is small. Then expression (281) is written as

∫ ∞ - - (− v2) An(x,z) ≈ n0 dv⊥v⊥exp ---⊥ 0[ ( 2) ] 1--N∑1 -1-N∑2 2π- q- × N1 N2 exp ιn LyΔ ρijy TδΦn (x + Δρijx,z) . (283) i=1 j=1

The approximation (282) makes the operator A_n on δΦ_n become local in z direction, i.e., it involves δΦ_n at locations with a ﬁxed value of z. This makes A_n(x,z) reduce to a 1D operator on δΦ_n in the x direction.

8.4 Using MC integration, to be continued, not necessary

The integration we try to express is given by

∫ Aijk ≈ -1-- dxnp (x ) Vijk∫Vijk ∫ ( ) -1-- -q ∂F0- = Vijk Vijk dx dv m (δΦ − ⟨δΦ ⟩α) ∂𝜀 , (284)

where A_ijk is the value of n_p(x) at a grid-point, which is approximated by the spatial averaging of n_p(x) over the cell whose center is the grid-point, V _ijk is the volume of the cell. We will use Monte-Carlo guiding-center markers to compute the above cell average.

( ) A(1) = −-q--1-∑ ∑ ⟨δΦ ⟩ ∂F0-1 ijk m Vijk p α α ∂𝜀 g ∑ ∑ ( ) = −-q--1- ⟨δΦ⟩α ∂F0-1 m Vijk p α ∂𝜀 g

Nearest neighbour interpolation

∑ ∑ ( ) A(2) = − q--1-- δΦ ∂F01 ijk m Vijk p α ∂𝜀 g q δΦ ∑ ∑ ( ∂F 1) = − ----ijk- --0- m Vijk p α ∂𝜀 g

Later, I found that evaluating the polarization density using grid works well. Therefore there is no need to evaluate it using MC markers, which is more complicated.

[next] [prev] [prev-tail] [front] [up]