[next] [prev] [prev-tail] [tail] [up]

3.4 Equation for macroscopic distribution function Fg

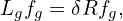
The evolution of the macroscopic quantity Fg is governed by Eq. (48), i.e.,

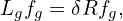LgFg = 0,
(63)

where the left-hand side is written as

∂Fg ∂X ∂Fg ∂V ∂Fg LgFg = -∂t-+ -∂t ⋅∂X--+ ∂t-⋅-∂V- ∂Fg ∂Fg + (v∥e∥ + VE0)⋅ ∂X-+ v ⋅[(λB1 + λB2)Fg]− Ω ∂α-- q (v⊥ ∂Fg eα ∂Fg) + --E0 ⋅ -------+ ------- m B0 ∂μ v⊥ ∂α
Expand Fg as Fg = Fg0 + Fg1 + …., where Fgi ∼ Fg0O(λi). Then, the balance on order O(λ0) gives
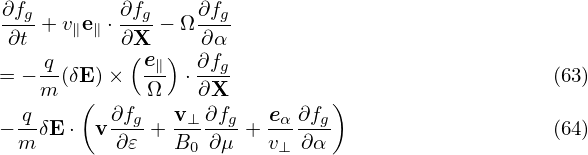∂Fg0 = 0 ∂α
(64)

i.e., Fg0 is independent of the gyro-angle α. The balance on O(λ1) gives

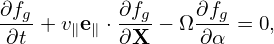( ) v e ⋅ ∂Fg0 +-qE ⋅ v-⊥∂Fg0 = Ω ∂Fg1 . ∥ ∥ ∂X m 0 B0 ∂μ ∂α
(65)

Performing averaging over α, ∫ 02π(…)dα, on the above equation and noting that Fg0 is independent of α, we obtain

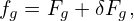(∫ 2π ) ∂Fg0 q ∂Fg0∫ 2π ( v⊥) ∫ 2π ∂Fg1 dαv∥e∥ ⋅∂X-- + m--∂μ- dαE0 ⋅ B-- = dα Ω-∂α- 0 0 0 0
(66)

Note that a quantity A = A(x) that is independent of v will depend on v when transformed to guiding-center coordinates, i.e., A(x) = Ag(X,v). Therefore Ag depends on gyro-angle α. However, since ρi∕L ≪ 1 for equilibrium quantities, the gyro-angle dependence of the equilibrium quantities can be neglected. Specifically, e∥, B0 and Ω can be considered to be independent of α. As to v∥, we have v∥ = ±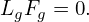∘ ---------- 2(𝜀− B0μ). Since B0 is considered independent of α, so does v∥. Using these results, equation (66) is written

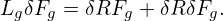∫ 2π ( ) v e ⋅ ∂Fg0+-q ∂Fg0 dαE0 ⋅ v⊥- = 0. ∥ ∥ ∂X m ∂ μ 0 B0
(67)

Using E0 = −∇Φ0, the above equation is written as

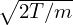∫ 2π ( ) v∥e∥ ⋅ ∂Fg0 + q-∂Fg0 dα − v⊥-⋅∇-Φ0 = 0, ∂X m ∂μ 0 B0
(68)

Note that

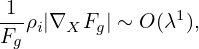∫ 2π 1 dα---v⊥ ⋅∇X Φ0 ≈ 0, 0 B0
(69)

where the error is of O(λ2)Φ0, and thus, accurate to O(λ), the last term of equation (68) is zero. Then equation (68) is written as

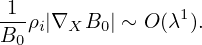v e ⋅ ∂Fg0 = 0, ∥ ∥ ∂X
(70)

which implies that Fg0 is constant along a magnetic field line.

[next] [prev] [prev-tail] [front] [up]