[next] [prev] [prev-tail] [tail] [up]

3.5 Equation for perturbed distribution function δFg

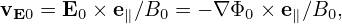
Using Fg ≈ Fg0, equation (49) is written as

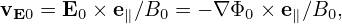LgδFg = δRFg0 + δR δFg , ◟-◝◜-◞ 2 NonlinearTerm ∼O(λ )
(71)

where δRδFg is a nonlinear term which is of order O(λ2) or higher, LgδFg and δRFg0 are linear terms which are of order O(λ1) or higher. The linear term δRFg0 is given by

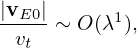( ) ( ) q- v-×-δB (e∥ ) ∂Fg0 q- ∂Fg0 v⊥-∂Fg0 δRFg0 = − m δE + c × Ω ⋅ ∂X − m δE ⋅ v ∂𝜀 + B0 ∂μ , ◟-------------◝◜2-------------◞ ◟----------◝◜1----------◞ O(λ ) O(λ )
(72)

In obtaining (72), use has been made of ∂Fg0∕∂α = 0. Another linear term LgδFg is written as

∂ δF ∂δF ∂ δF Lg δFg =----g+ (v∥e∥ + VE0 )⋅--g-+ v⋅[λB1 + λB2 ]δFg − Ω---g ∂t ∂X ◟-∂◝α◜-◞ ( ) O(λ1) -q v⊥-∂δFg- -eα∂δFg- + m E0 ⋅ B0 ∂ μ + v⊥ ∂α , (73)
where Ω∂δFg∕∂α is of order O(λ1) and all the other terms are of order O(λ2).

Next, to reduce the complexity of algebra, we consider the easier case in which ∂Fg0∕∂μ = 0.

Balance on order O(λ1): adiabatic response

The balance between the leading terms (terms of O(λ)) in Eq. (71) requires that

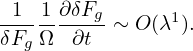( ) ∂-δFa- q- ∂Fg0 Ω ∂α = m δE ⋅ v ∂𝜀 ,
(74)

where δFa is a unknown distribution function to be solved from the above equation. It is ready to verify that

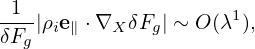δF = q-δΦ∂Fg0 , a m ∂𝜀
(75)

is a solution to the above equation, accurate to O(λ). [Proof: Substitute expression (75) into the left-hand side of Eq. (74), we obtain

( ) ∂δFa- ∂-- q- ∂Fg0 Ω ∂α = Ω ∂α m δΦ ∂𝜀 q ∂Fg0 ∂ = m--∂𝜀-Ω ∂α-(δΦ ) q ∂F ∂x = ----g0Ω (∇xδΦ) ⋅--- (76) m ∂𝜀 ∂α
Using
∂x ∂ [ e∥(X )] ∂α-= ∂α-− v × Ω(X-)- = ∂-[− v]× e∥(X-) ∂α Ω(X ) = − v⊥- (77) Ω
Eq. (76) is written as
∂δF q ∂F v Ω ---a-= − ----g0Ω(∇x δΦ)⋅-⊥- ∂α m ∂𝜀( )Ω = q-∂Fg0 δE + ∂δA- ⋅v⊥ (78) m ∂𝜀 ∂t ≈ q-∂Fg0(δE) ⋅v⊥, (79) m ∂𝜀
where terms of O(λ2) have been dropped. Similarly, dropping the parallel electric field term (which is of O(λ2)) on the right-hand side of Eq. (74), we find it is identical to the right-hand side of Eq. (79)]
Separate δFg into adiabatic and non-adiabatic part

As is discussed above, the terms of O(λ) can be eliminated by splitting a so-called adiabatic term form δFg. Specifically, write δFg as

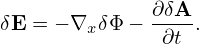δFg = δFa + δG,
(80)

where δFa is given by (75), i.e.,

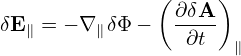δF = q-δΦ∂Fg0 , a m ∂𝜀
(81)

which depends on the gyro-angle via δΦ and this term is often called adiabatic term. Plugging expression (80) into equation (71), we obtain

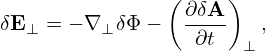LgδG = δRFg0 − LgδFa+ δR δFg . ◟-Linea◝◜rTerms-◞ Non◟li ◝ne◜arT◞erms
(82)

Next, let us simplify the linear term on the right-hand side, i.e, δRFg0 −LgfδFa, (which should be of O(λ2) or higher because Ω∂δFa∕∂α cancels all the O(λ1) terms in δRFg0).

LgδFa is written

LgδFa = q-∂Fg0LgδΦ + q-δΦLg∂Fg0 m ∂𝜀 m ∂ 𝜀 ≈ q-∂Fg0LgδΦ, (83) m ∂𝜀
where the error is of order O(λ3). In obtaining the above expression, use has been made of e∥⋅∂Fg0∕∂X = 0, ∂Fg0∕∂X = O(λ1)Fg0, ∂Fg0∕∂α = 0, ∂Fg0∕∂μ = 0, and the definition of λB1 and λB2 given in expressions (20) and (21). The expression (83) involves δΦ operated by the Vlasov propagator Lg. Since δΦ takes the most simple form when expressed in particle coordinates (if in guiding-center coordinates, δΦ(x) = δΦ(X−v ×e∥∕Ω), which depends on velocity coordinates and thus more complicated), it is convenient to use the Vlasov propagator Lg expressed in particle coordinates. Transforming Lg back to the particle coordinates, expression (83) is written
q ∂F [ ∂δΦ q ∂Φ ] LgδFa = ----g0 ---|x,v + v⋅∇x δΦ+ --(E0 + v× B0 )⋅---|x m ∂𝜀 [ ∂t ] m ∂v = q-∂Fg0 ∂δΦ|x,v + v⋅∇x δΦ (84) m ∂𝜀 [ ∂t ( )] q-∂Fg0 ∂δΦ- ∂δA- = m ∂𝜀 ∂t |x,v + v⋅ − δE − ∂t |x,v q ∂F [ ∂δΦ ∂v ⋅δA ] = ----g0 ---|x,v − v⋅δE − ------|x,v . (85) m ∂𝜀 [ ∂t ∂t] = q-∂Fg0 ∂δΦ-− v⋅δE − ∂v-⋅δA- . (86) m ∂𝜀 ∂t ∂t
Using this and expression (72), δRFg0 − LgδFa is written as
( ) ( ) δRFg0 − LgδFa = − q(δE + v ×δB )× e∥ ⋅ ∂Fg0 − q-δE ⋅ v∂Fg0 m [ Ω ∂X ] m ∂ 𝜀 − q-∂Fg0 ∂δΦ-− v⋅δE − ∂v-⋅δA- m ∂𝜀 ∂t ∂t q (e∥) ∂Fg0 q ∂Fg0 [∂Φ ∂v ⋅δA ] = − m(δE + v ×δB )× -Ω ⋅-∂X- − m--∂𝜀- ∂t-− --∂t--- , (87)
where the two terms of O(λ1) (the terms in blue and red) cancel each other, with the remain terms being all of O(λ2), i.e, the contribution of the adiabatic term cancels the leading order terms of O(λ1) on the RHS of Eq. (82).

The consequence of this is that, as we will see in Sec. 3.6, δG is independent of the gyro-angle, accurate to order O(λ1). Therefore, separating δF into adiabatic and non-adiabatic parts also corresponds to separating δF into gyro-angle dependent and gyro-angle independent parts.

Linear term expressed in terms of δΦ and δA

Let us rewrite the linear term (87) in terms of δΦ and δA. The δE + v ×δB term in expression (87) is written as

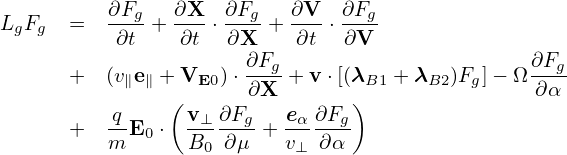∂δA- δE +v × δB = − ∇x δΦ − ∂t + v × ∇x × δA.
(88)

Note that this term needs to be accurate to only O(λ). Then

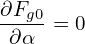δE + v× δB ≈ − ∇xδΦ + v× ∇x × δA,
(89)

where the error is of O(λ2). Using the vector identity v ×∇x ×δA = (∇δA) ⋅v − (v ⋅∇)δA and noting v is constant for ∇x operator, the above equation is written

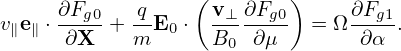δE + v × δB = − ∇x δΦ+ ∇x (δA ⋅v )− (v ⋅∇x )δA
(90)

Note that Eq. (22) indicates that ∇xδΦ ≈∇XδΦ, where the error is of O(λ2), then the above equation is written

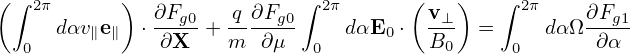δE+ v × δB = − ∇ δΦ + ∇ (δA ⋅v)− (v⋅∇ )δA X X X
(91)

Further note that the parallel gradients in the above equation are of O(λ2) and thus can be dropped. Then expression (91) is written

δE + v× δB = − ∇ δΦ+ ∇ (δA ⋅v) − (v ⋅∇ )δA. X ⊥ X⊥ ⊥ X⊥ = − ∇X ⊥δL− v ⊥ ⋅∇X ⊥δA, (92)
where δL is defined by
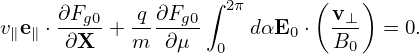δL = δΦ − v ⋅δA.
(93)

Using expression (92), equation (87) is written

[ ] δRF0 − LgδFa = − q- (− ∇X ⊥δL − v⊥ ⋅∇X ⊥δA) × e∥ ⋅ ∂Fg0 −-q∂δL-∂Fg0, m Ω ∂X m ∂t ∂𝜀
(94)

where all terms are of O(λ2).

[next] [prev] [prev-tail] [front] [up]