Expressing the perturbed drift in terms of δE and δB

E.3 Expressing the perturbed drift in terms of δE and δB

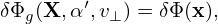
The perturbed drift δV_D is given by Eq. (122), i.e.,

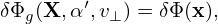q e∥ δVD = −m-∇X ⟨δL⟩α × Ω-.

(293)

Using δL = δΦ − v ⋅ δA, the above expression can be further written as

δV = −-q∇ ⟨δΦ − v⋅δA ⟩ × e∥ D m X α Ω = q-e∥ ×∇X ⟨δΦ⟩α − q-e∥ ×∇X ⟨v∥δA∥⟩α m Ω m Ω −-q e∥× ∇X ⟨v⊥ ⋅δA ⊥⟩α. (294) m Ω

Accurate to order O(λ), the term involving δΦ is

e e -q -∥× ∇X ⟨δΦ⟩α = -∥-×⟨∇X δΦ⟩α m Ω Be0 ≈ -∥-×⟨∇x δΦ⟩α B0 ⟨ ⟩ ≈ e∥-× − δE − ∂δA B0 ∂t α e∥- ≈ B0 ×⟨− δE⟩α ≡ δVE, (295)

which is the δE×B₀ drift. Accurate to O(λ), the ⟨v_∥δA_∥⟩_α term on the right-hand side of Eq. (294) is written

− q-e∥× ∇X ⟨v∥δA∥⟩α ≈ − q-1⟨e∥ × ∇X (v∥δA ∥)⟩α m Ω m Ω ≈ − q--1⟨e∥ × ∇x (v∥δA∥)⟩α m Ωv ≈ − q--∥⟨e∥ × ∇x (δA ∥)⟩α m Ω = v∥⟨δB-⊥⟩α, (296) B0

which is due to the magnetic ﬂuttering (this is actually not a real drift). In obtaining the last equality, use has been made of Eq. (287), i.e., δB_⊥ = ∇_xδA_∥× e_∥.

Accurate to O(λ), the last term on the right-hand side of expression (294) is written

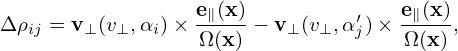
− q-e∥× ∇X ⟨v⊥ ⋅δA⊥ ⟩α ≈ − 1-⟨e∥ × ∇X (v⊥ ⋅δA⊥ )⟩α m Ω B0 ≈ − 1-⟨e × ∇ (v ⋅δA )⟩ B0 ∥ x ⊥ ⊥ α 1-- = − B0⟨e∥ × (v⊥ × ∇x ×δA ⊥ + v⊥ ⋅∇xδA ⊥)⟩α 1-- = − B0⟨(e∥ ⋅∇x × δA⊥ )v ⊥ + e∥ × v ⊥ ⋅∇x δA⊥ ⟩α

Using equation (289), i.e., δB_∥ = e_∥⋅∇× δA_⊥, the above expression is written as

−-q e∥× ∇ ⟨v ⋅δA ⟩ = − 1-⟨δB v + e × v ⋅∇ δA ⟩ m Ω X ⊥ ⊥ α B0 ∥ ⊥ ∥ ⊥ x ⊥ α 1-- ≈ − B0⟨δB∥v⊥ + e∥ × v⊥ ⋅∇X δA⊥ ⟩α 1 1 ≈ − B0⟨δB∥v⊥ ⟩α − B0e∥ × ⟨v ⊥ ⋅∇X δA ⊥⟩α. 1 ≈ − B-⟨δB∥v⊥ ⟩α. (297) 0

where use has been made of ⟨v_⊥⋅∇_XδA_⊥⟩_α ≈ 0 (**seems wrong**), where the error is of O(λ)δA_⊥. The term ⟨δB_∥v_⊥⟩_α∕B₀ is of O(λ²) and thus can be neglected (I need to verify this).

Using Eqs. (295), (296), and (297), expression (294) is ﬁnally written as

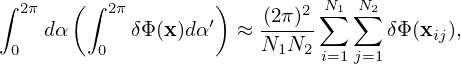q e ⟨δE⟩ × e ⟨δB ⟩ δVD ≡ − --∇X ⟨δL ⟩α × -∥ = ----α---∥-+ v∥---⊥-α. m Ω B0 B0

(298)

Using this, the ﬁrst equation of the characteristics, equation (119), is written as

dX-= v∥e∥ + VD + δVD (299) dt = ve + V + ⟨δE⟩α ×-e∥-+ v ⟨δB-⊥⟩α- ∥ ∥ D B0 ∥ B0 ≡ VG (300)

[next] [prev] [prev-tail] [front] [up]