[prev] [prev-tail] [tail] [up]

E.4 Expressing the coefficient before ∂F0∕∂𝜀 in terms of δE and δB

[Note that

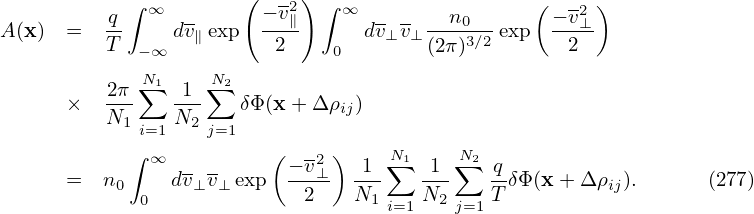
∂δA⊥-= − (δE ⊥ + ∇⊥δΦ ), ∂t
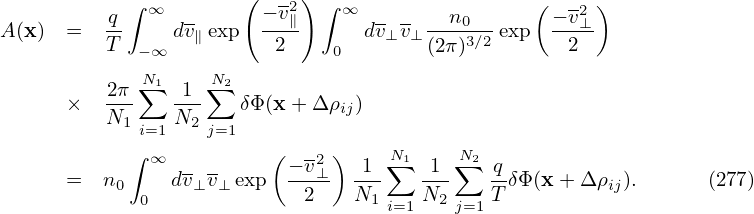(301)

where ∂δA⊥∕∂t is of O(λ2). This means that δE⊥ + ∇⊥δϕ is of O(λ2) although both δE⊥ and δϕ are of O(λ).]

Note that

∂⟨v ⋅δA⟩α ∂⟨δA∥⟩α ∂ ⟨δA ⟩α --------- = v∥-------+ v ⊥ ⋅------ ∂t ∂⟨∂δtA ⟩ ∂t = v∥----∥-α+ ⟨v⊥ ⋅(− δE − ∇δΦ )⟩α ∂t ≈ v∥∂⟨δA∥⟩α− ⟨v⊥ ⋅δE⟩α (302) ∂t
where use has been made of ⟨v⊥⋅∇δϕ⟩≈ 0, This indicates that ⟨v⊥⋅ δE⟩α is of O(λ1)δE. Using Eq. (302), the coefficient before ∂F0∕∂𝜀 in Eq. (138) can be further written as
q [ ∂ ⟨v ⋅δA⟩α ( q e∥ ) ] − m- −----∂t--- − v∥e∥ + VD − m-Ω-× ∇X ⟨v ⋅δA ⟩α ⋅∇X ⟨δΦ⟩α [ ( ) ⟨ ⟩ ] = − q- − v∥∂⟨δA-∥⟩α + ⟨v⊥ ⋅δE ⟩α − v∥e∥ + VD − q-e∥× ∇X ⟨v ⋅δA ⟩α ⋅ − δE − ∂δA m [ ∂t m Ω ∂t⟨ α ⟩ ] q- ∂⟨δA-∥⟩α ( q-e∥ ) ∂A∥- ≈ − m − v∥ ∂t + ⟨v⊥ ⋅δE ⟩α − v∥e∥ + VD − m Ω × ∇X ⟨v ⋅δA ⟩α ⋅⟨− δE⟩α + v∥ ∂t q [ ( q e∥ ) ] α = − m- ⟨v ⊥ ⋅δE ⟩α + v∥e∥ + VD − m Ω-× ∇X ⟨v⋅δA ⟩α ⋅⟨δE⟩α q [ ( ⟨δB ⟩) ] ≈ − -- ⟨v⊥ ⋅δE ⟩α + v∥e∥ + VD + v∥---⊥-- ⋅⟨δE⟩α . (303) m B0
Using Eq. (303) and (), gyrokinetic equation (138) is finally written as
[ ∂ ( ⟨δE ⟩α × e∥ ⟨δB⊥ ⟩α ) ] ∂t + v∥e∥ + VD +----B-----+ v∥--B---- ⋅∇X δf ( 0 ) 0 = − ⟨δE⟩α-×-e∥+ v∥⟨δB⊥-⟩α- ⋅∇XF0 [ B0 ( B0 ) ] q- ⟨δB-⊥⟩α- ∂F0- − m ⟨v⊥ ⋅δE ⟩α + v∥e∥ + VD + v∥ B0 ⋅⟨δE⟩α ∂𝜀 . (304)

[prev] [prev-tail] [front] [up]