[next] [prev] [prev-tail] [tail] [up]

3.2 Cell-averaged velocity moment

One of the most important methods of reducing collisions between markers when using very few markers to approximate a system with much more physical particles is to solve Maxwell’s equation on discrete grids and use the cell-averaged moments obtained from markers as the source term in the field equation.

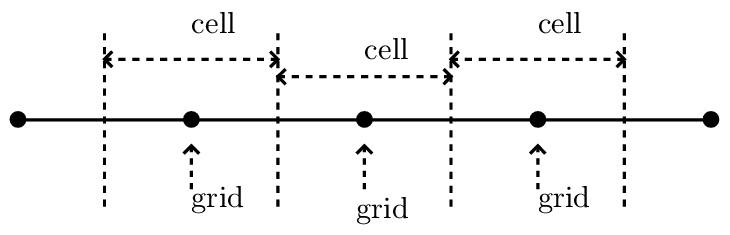
To be clear, grid points and the corresponding cells are defined as illustrated in Fig. 2 for the 1D case.

pict

Figure 2: Definition of spatial grid points and cells in PIC simulations. A grid point is the center of the corresponding cell.

Field solvers in PIC code need the values of I at the grid-points. This value at the grid point is defined as the average of I over the corresponding cells (similar to that in the finite element method), i.e.,

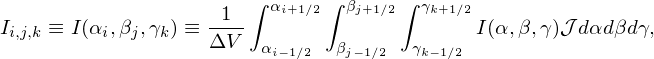∫ αi+1∕2∫ βj+1∕2∫ γk+1∕2 Ii,j,k ≡ I(αi,βj,γk) ≡-1-- I(α, β,γ)𝒥 dαdβdγ, ΔV αi−1∕2 βj−1∕2 γk−1∕2
(37)

where ΔV = ∫ αi−1∕2αi+1∕2 ∫ βj−1∕2βj+1∕2 ∫ γk−1∕2γk+1∕2 𝒥dαdβdγ is the cell volume, which can be approximated as ΔV ≈𝒥i,j,kΔαΔβΔγ. Using Eqs. (36), the above expression is written as

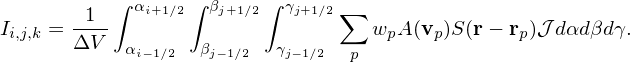∫ α ∫ β ∫ γ I = -1-- i+1∕2 j+1∕2 j+1∕2∑ w A(v )S(r− r )𝒥 dαdβdγ. i,j,k ΔV αi−1∕2 βj−1∕2 γj−1∕2 p p p p
(38)

Using the shape function given in expression (25), the above expression is written as

∫ ∫ ∫ [ ( ) ][ ( ) ][ ( )] -1--∑ αi+1∕2 βj+1∕2 γj+1∕2 --1- α−-αp- --1- β-−-βp -1-- γ-− γp Ii,j,k = ΔV wpA (vp) αi−1∕2 βj−1∕2 γj−1∕2 Δ αpS1D Δαp Δ βpS1D Δ βp Δ γpS1D Δ γp dαd βdγ, p
(39)

where the Jacobian in the integrand is cancelled out. The 3D integral in expression (39) consists of three identical 1D integrations. Consider one of them:

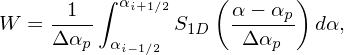( ) --1-∫ αi+1∕2 α−-αp- W = Δ αp α S1D Δαp dα, i−1∕2
(40)

Consider the case Δαp = Δα, and choose S1D to be the l th order b-spline function, bl, then the above expression is written as

∫ ( ) W = -1- αi+1∕2 b α-− αp dα (41) Δ α αi−1∕2 l Δ α (α − α ) = bl+1 --i---p , (42) Δ α
where bl+1 is the (l + 1)th order b-spline function. [Proof of Eq. (42): Using the property of the zeroth order b-spline function b0 (a flat top function), the integration (41) can be written as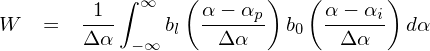
1 ∫ ∞ ( α − αp) (α − αi) W = Δ-α bl -Δ-α-- b0 --Δα-- dα −∞
By using the definition of the b-splines, we find the above expression is a b-spline function that is one order higher than the corresponding b-spline shape function, i.e.,
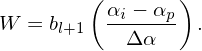
( αi − αp) W = bl+1 -Δ-α--- .

] Therefore expression (39) is written as

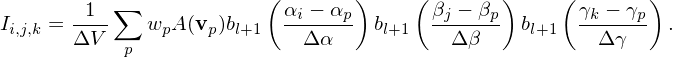( ) ( ) ( ) -1--∑ αi-−-αp βj −-βp γk-−-γp- Ii,j,k = ΔV wpA (vp)bl+1 Δ α bl+1 Δβ bl+1 Δ γ . p
(43)

Recall that, in terms of the b-spline functions, the local value I(α,β,γ) is given by expression (36), i.e.,

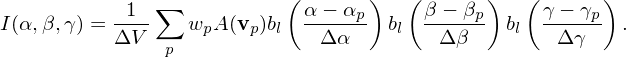1 ∑ (α − αp) (β − βp) ( γ − γp ) I(α,β,γ ) = ΔV- wpA(vp)bl --Δα-- bl --Δβ-- bl -Δ-γ-- . p
(44)

It is instructive to compare expression (43) with (44), which indicates that they are similar except that the b-spline functions involved in the cell-averaged expression (43) is one order higher than that involved in the local expression (44).

[next] [prev] [prev-tail] [front] [up]