3.4 Effective force on a marker

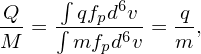
The total charge of a group of particles represented by a maker, Q, is given by Q = ∫ qf_pd⁶v, where q is the charge of a single particle. Then the effective force on a marker is then F_p = QE_p with E_p given by Eq. (??). The total mass of a group of particles represented by a marker, M, is given by M = ∫ mf_pd⁶v, where m is the mass of a single particle. Then the ratio between Q and M is written as

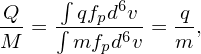(50)

which is identical to the single particle charge mass ratio. Note that the motion equation of a particle in an electromagnetic field is distinguished only by this ratio. Therefore motion of a marker in the phase space is identical with the motion of a real particle with the effective field given by Eq. (??).