1.9 Closed magnetic surfaces in tokamak

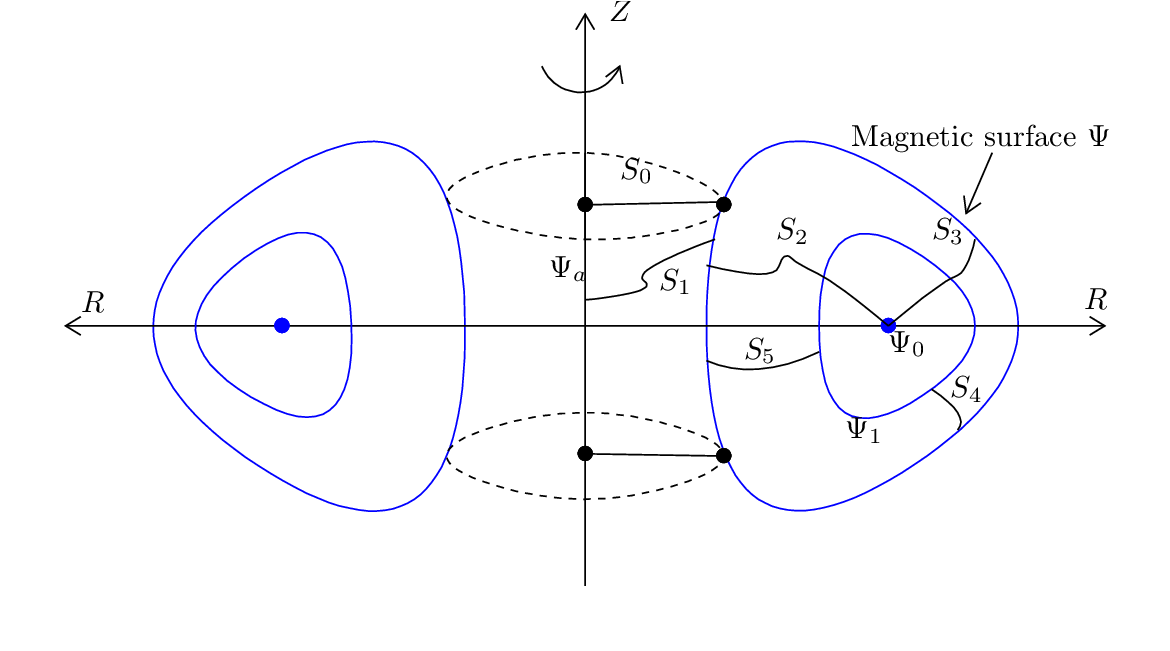
In most part of a tokamak plasma, the contours of Ψ on (R,Z) plane are closed curves. As discussed above, the contours of Ψ are the projection of magnetic lines on the poloidal plane. Closed contours of Ψ implies closed magnetic surfaces, as shown in Fig 3.

The innermost magnetic surface reduces to a curve, which is called magnetic axis (in Fig. 3, Ψ₀ labels the magnetic axis). Because the magnetic axis is the point of maximum/minimum of Ψ(R,Z), the value of ∇Ψ is zero at the magnetic axis. As a result, the poloidal component of the equilibrium magnetic field is zero on magnetic axis (refer to Eq. (10)), i.e., the magnetic field has only toroidal component there.

As discussed in Sec. 1.7, the poloidal magnetic flux enclosed by a magnetic surface Ψ (the poloidal magnetic flux through the toroidal surfaces S₂) is given by

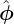(27)

where Ψ₀ is the value of Ψ at the magnetic axis. Here the positive direction of the surface S₂ is defined to be in the clockwise direction when an observer looks along the direction of 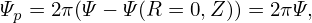. In practice, we need to pay attention to the positive direction of the toroidal surface used to define the poloidal flux (there can be a sign difference when choosing different positive directions). Also note, in tokamak literature, the poloidal magnetic flux enclosed by a closed magnetic surface can have two different definitions, one of which is the the poloidal magnetic flux through the surface S₂ in Fig. 3, the other one is the poloidal magnetic flux through the central hole of the magnetic surface, i.e., the poloidal flux through S₁ in Fig. 3. The former definition is adopted in this article, except explicitly specified otherwise. In the latter case, the poloidal magnetic flux is written

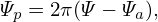(28)

where the positive direction of the surface S₁ is defined to be in the clockwise direction.

Also note that, since the poloidal magnetic field can be written as B_p = ∇Ψ ×∇ϕ, the condition Ψ_LCFS − Ψ_axis > 0 means B_p points in the anticlockwise direction (viewed along ϕ direction), and Ψ_LCFS − Ψ_axis < 0 means B_p points in the clockwise direction.

Shape parameters of a closed magnetic surface

Let us introduce parameters characterizing the shape of a magnetic surface in the poloidal plane. The “midplane” is defined as the plane that passes through the magnetic axis and is perpendicular to the symmetric axis (Z axis). For a up-down symmetric (about the midplane) magnetic surface, its shape can be roughly characterized by four parameters, namely, the R coordinate of the innermost and outermost points in the midplane, R_in and R_out; the (R,Z) coordinators of the highest point of the magnetic surface, (R_top,Z_top). These four parameters are indicated in Fig. 4.

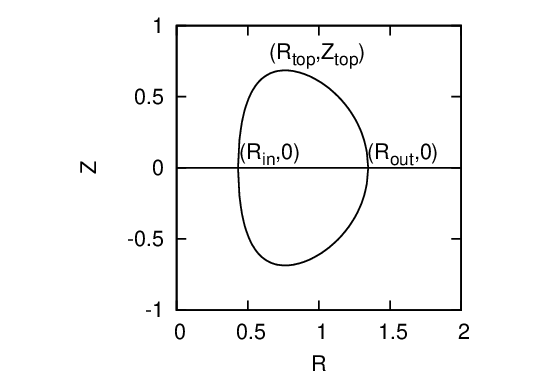
In terms of these four parameters, we can define the major radius of a magnetic surface

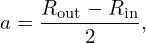(29)

(which is the R coordinate of the geometric center of the magnetic surface), the minor radius of a magnetic surface

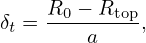(30)

the triangularity of a magnetic surface

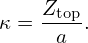(31)

and, the ellipticity (elongation) of a magnetic surface

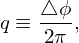(32)

Usually, we specify the value of R₀, a, δ_t, and κ, instead of (R_in,R_out,R_top,Z_top), to characterize the shape of a magnetic surface. The value of the triangularity δ_t is usually positive in traditional tokamak operations, but negative triangularity is achievable and potentially useful, which is under active investigation.

Besides, using a and R₀, we can define another useful parameter 𝜀 ≡ a∕R₀, which is called the inverse aspect ratio.

The four shape parameters for the typical Last-Closed-Flux-Surface (LCFS) of EAST tokamak are: major radius R₀ = 1.85m (can reach 1.9m), minor radius a = 0.45m, ellipticity κ = 1.8 (can be in the range from 1.7 to 1.9), triangularity δ_t = 0.6 (can be in the range from 0.5 to 0.7). Note that the major radius R₀ of the LCFS is usually different from R_axis (the R coordinate of the magnetic axis). Usually we have R_axis > R₀ due to the so-called Shafranov shift.