[next] [prev] [prev-tail] [tail] [up]

1.5 Contours of Ψ in the poloidal plane

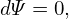
Because Ψ is constant along a magnetic field line and Ψ is independent of ϕ, it follows that the projection of a magnetic field line onto (R,Z) plane is a contour of Ψ. On the other hand,  are contours of Ψ on (R,Z) plane also the projections of magnetic field lines onto the plane? Yes, they are. [Proof. A contour of Ψ on (R,Z) plane satisfies

dΨ = 0,
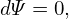(15)

i.e.,

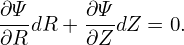∂Ψ ∂Ψ ∂R-dR + ∂Z-dZ = 0.
(16)

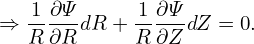1 ∂Ψ 1∂Ψ ⇒ ----dR + -----dZ = 0. R∂R R ∂Z
(17)

Using Eqs. (5) and (6), the above equation is written

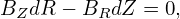BZdR − BRdZ = 0,
(18)

i.e.,

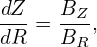dZ- BZ- dR = BR ,
(19)

which is the equation of the projection of a magnetic field line on (R,Z) plane. Thus, we prove that contours of Ψ are also the projections of magnetic field lines in (R,Z) plane.]

[next] [prev] [prev-tail] [front] [up]