[next] [prev] [prev-tail] [tail] [up]

1.8 Measurement of poloidal magnetic flux

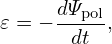
By measuring the voltage around a toroidal loop of wire, we can obtain the time derivative of the poloidal magnetic flux though the loop and, after integrating over time, the poloidal magnetic flux itself. Suppose that the loop is located at (R,Z) and denote the magnetic flux through the loop by Ψpol(R,Z,t) (only the poloidal magnetic field contribute to this flux since the loop is in the toroidal direction). Then Faraday’s law gives

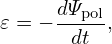𝜀 = − dΨpol, dt
(21)

where 𝜀 is the emf. If the loop is a coil with N turns, the induced voltage V in the coil is N times the emf 𝜀, i.e., V = N𝜀. Using this, Eq. (21) is written as

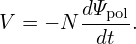dΨ V = − N --pol. dt
(22)

Integrating the above equation over time, we obtain

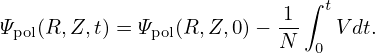∫ t Ψpol(R,Z,t)− Ψpol(R,Z, 0) = − 1 Vdt. N 0
(23)

The starting time t = 0 can be chosen at a time when no plasma is present and thus the initial value, Ψpol(R,Z,0), is easy to obtain.

As discussed in Sec. 1.7 ,the relation between Ψ and Ψpol is given by

Ψpol(R,Z,t) = 2π[Ψ(R,Z,t)− Ψ(R = 0,Z,t)],
(24)

where Ψ(R = 0,Z,t) is actually a spatial constant since R = 0 must be a magnetic field line (required by the axisymmetry). Ψ(R = 0,Z,t) is also a time constant if we choose a gauge that is independent of time. We will stick to the time-independent gauge since it does not seem useful to choose a time-dependent gauge for Ψ. Denote the spatial-temporal constant Ψ(R = 0,Z,t) by Cg, then Eq. (24) is written as

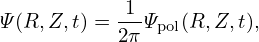1 Ψ(R,Z,t) =---Ψpol(R,Z,t)+ Cg, 2π
(25)

i.e.,

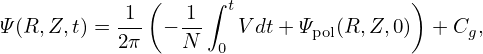( ∫ ) -1- -1 t Ψ(R,Z,t) = 2π − N 0 V dt+ Ψpol(R,Z,0) + Cg,
(26)

which tells us how to obtain Ψ form the measured voltage V .

The above toroidal loop of wire used to measure poloidal magnetic flux is often called “flux loop” by tokamak operators. There are usually many flux loops (e.g. 37 on EAST[30], 41 on DIII-D) at different locations in the poloidal plane (see Fig. 33). The measured value of poloidal flux can be used to obtain contours of Ψ and thus obtain a flux surface. With the feedback control (by adjusting the current in the poloidal field coils), these measurement, along with the poloidal field measurement by magnetic probes, can be used to control the shape of the last-closed-flux-surface (LCFS), the distance of the LCFS from the first wall, and the X-point location. This is often called iso-flux control, gap control, or X-point control.

[next] [prev] [prev-tail] [front] [up]